INVESTIGATING RATE OF CHANGE

A rate of change is a ratio of the amount of change in the dependent variable to the amount of change in the independent variable.

Example 1 :

Eve keeps a record of the number of lawns she has mowed and the money she has earned. Tell whether the rates of change are constant or variable.

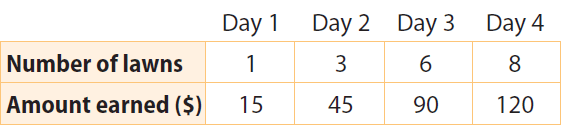
Solution :

Step 1 :

Identify the independent and dependent variables.

Independent : Number of lawns

Dependent : Amount earned

Step 2 :

Find the rates of change.

Day 1 to Day 2 :

Change in $/Change in lawns  =  (45 - 15)/(3 - 1) 

Change in $/Change in lawns  =  30/2 

Change in $/Change in lawns  =  15

Day 2 to Day 3 :

Change in $/Change in lawns  =  (90 - 45)/(6 - 3) 

Change in $/Change in lawns  =  45/3 

Change in $/Change in lawns  =  15

Day 3 to Day 4 :

Change in $/Change in lawns  =  (120 - 90)/(8 - 6) 

Change in $/Change in lawns  =  30/2 

Change in $/Change in lawns  =  15

The rates of change are constant : $15 per lawn.

Example 2 :

The table shows the approximate height of a football after it is kicked. Tell whether the rates of change are constant or variable.

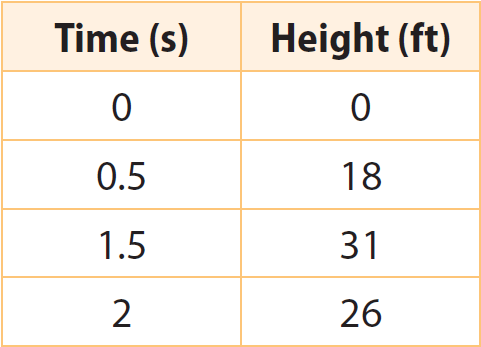
Solution :

Step 1 :

Identify the independent and dependent variables.

Independent : Time

Dependent : Height

Step 2 :

Find the rates of change.

0 seconds to 0.5 seconds :

Change in height/Change in time  =  (18 - 0)/(0.5 - 0) 

Change in height/Change in time  =  18/0.5 

Change in height/Change in time  =  36 

0.5 seconds to 1.5 seconds :

Change in height/Change in time  =  (31 - 18)/(1.5 - 0.5) 

Change in height/Change in time  =  13/1 

Change in height/Change in time  =  13 

1.5 seconds to 2 seconds :

Change in height/Change in time  =  (26 - 31)/(2 - 1.5) 

Change in height/Change in time  =  -5/0.5 

Change in height/Change in time  =  -10 

The rate of change are variable.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.