INVESTIGATING INEQUALITIES

We know that when we perform any of the four basic operations on both sides of an equation, the resulting equation is still true.

When we do the same thing in inequalities, the resulting inequality will still be true ?

Let us get answer to this question in the next section. 

Question 1 :

What effect does performing these operations on both sides of an inequality have ?

Answer : 

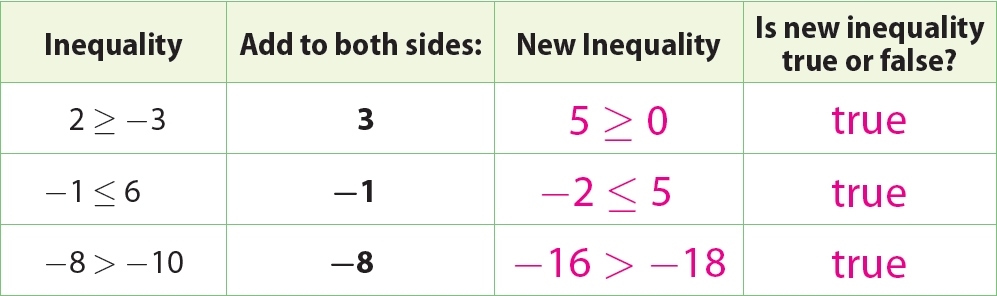
To get answer for the above question, let us look at the table given below. 

Question 2 :

When you add the same number to both sides of an inequality, is the inequality still true ? Explain how you know that your conjecture holds for subtracting the same number.

Answer : 

Yes; subtracting a number is the same as adding its opposite.

Question 3 :

Look at the table given below. 

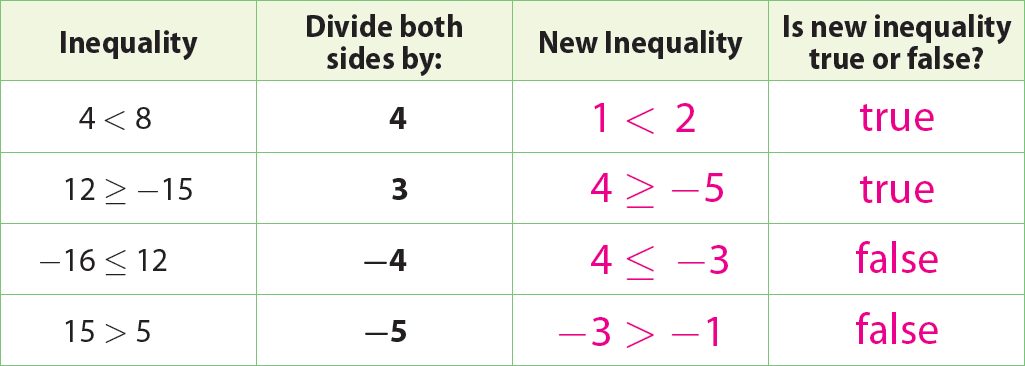
What do you notice when you divide both sides of an inequality by the same negative number ?

Answer : 

The inequality is no longer true.

Question 4 :

What could you do to make the inequalities that are not true into true statements ?

Answer : 

Reverse the inequality symbol.

Question 5 :

Explain how you know that your conjecture holds for multiplying both sides of an inequality by a negative number.

Answer : 

Multiplying by a number is the same as dividing by its reciprocal.

Question 6 :

In the inequality 3 > 2, if you multiply both sides by a positive number, do you have to reverse the inequality symbol ?

Answer : 

For example, if both sides of the inequality are multiplied by a positive number, say 4, we get 

3 x 4  >  2 x 4

12  >  8

When both sides of the inequality are multiplied by a positive number, still the inequality is true.

So we don't have to reverse the inequality symbol.  

Question 7 :

In the inequality -2 < 7 , if you multiply both sides by a negative number, do you have to reverse the inequality symbol ?

Answer : 

For example, if both sides of the inequality are multiplied by a negative number, say -3, we get 

(-2) x (-3)  <  7 x (-3)

6  <  -21

When both sides of the inequality are multiplied by a negative number, the resulting inequality is not true. 

To make the resulting inequality true, we have to reverse the inequality symbol. 

That is, 

6 > -21

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.