INVERSES OF SIN COS AND TAN

Inverses of sin, cosine and tangent functions takes the ratio of corresponding functions and gives the angle measure θ.

Trigonometric Ratio Table

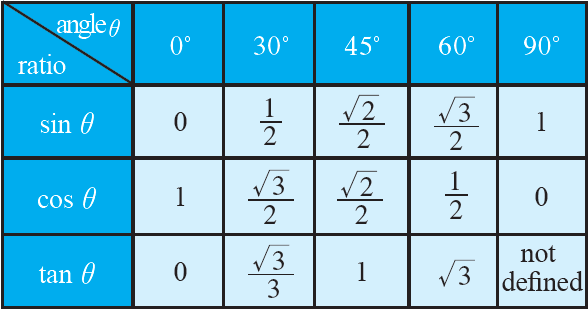
From the trigonometric ratio table above, we have

sin0° = cos90° = 0

sin90° = cos0° = 1

sin30° = cos60° = 1/2

sin60° = cos30° = √3/2

sin45° = cos45° = √2/2

sin0° = tan0° = 0

Examples 1-5 : If θ is an acute angle, find the value of θ in degrees.

Example 1 :

sin θ = 1/2

Solution :

sin θ = 1/2

θ = sin^-1(1/2) ----(1)

From the table above, we have

sin 30° = 1/2

30° = sin^-1(1/2) ----(2)

From (1) and (2),

θ = 30°

Example 2 :

tanθ = √3

Solution :

tanθ = √3

θ = tan^-1(√3) ----(1)

From the table above, we have

tan60° = √3

60° = tan^-1(√3) ----(2)

From (1) and (2),

θ = 60°

Example 3 :

cosθ = √2/2

Solution :

cosθ = √2/2

θ = cos^-1(√2/2) ----(1)

From the table above, we have

45° = cos^-1(√2/2) ----(2)

From (1) and (2),

θ = 45°

Example 4 :

sinθ = √2/2

Solution :

sinθ = √2/2

θ = sin^-1(√2/2) ----(1)

From the table above, we have

sin45° = √2/2

45° = sin^-1(√2/2) ----(2)

From (1) and (2),

θ = 45°

Example 5 :

cosθ = √3/2

Solution :

cosθ = √3/2

θ = cos^-1(√3/2) ----(1)

From the table above, we have

cos30° = √3/2

30° = cos^-1(√3/2) ----(2)

From (1) and (2),

θ = 30°

Examples 6-10 : If θ is an acute angle, find the value of θ in radians.

Example 6 :

sinθ = √3/2

Solution :

sinθ = √3/2

θ = sin^-1(√3/2) ----(1)

From the table above, we have

sin60° = √3/2

60° = sin^-1(√3/2) ----(2)

From (1) and (2),

θ = 60°

To convert degrees to radians, multiply by π/180°.

θ = 60° ⋅ (π/180°)

θ = π/3

Example 7 :

cosθ = 1/2

Solution :

cosθ = 1/2

θ = cos^-1(1/2) ----(1)

From the table above, we have

cos60° = 1/2

60° = cos^-1(1/2) ----(2)

From (1) and (2),

θ = 60°

To convert degrees to radians, multiply by π/180°.

θ = 60° ⋅ (π/180°)

θ = π/3

Example 8 :

tanθ = √3/3

Solution :

tanθ = √3/3

θ = tan^-1(√3/3) ----(1)

From the table above, we have

tan30° = √3/3

30° = tan^-1(√3/3) ----(2)

From (1) and (2), 

θ = 30°

To convert degrees to radians, multiply by π/180°.

θ = 30° ⋅ (π/180°)

θ = π/6

Example 9 :

tanθ = 1

Solution :

tanθ = 1

θ = tan^-1(1) ----(1)

From the table above, we have

45° = tan^-1(1) ----(2)

From (1) and (2),

θ = 45°

To convert degrees to radians, multiply by π/180°.

θ = 45° ⋅ (π/180°)

θ = π/4

Example 10 :

tan θ = 1/0

Solution :

tan θ = 1/0

θ = tan^-1(1/0) ----(1)

From the table above, we have

tan90° = not defined

tan90° = 1/0

 90° = tan-1(1/0) ----(2)

From (1) and (2),

θ = 90°

To convert degrees to radians, multiply by π/180°.

θ = 90° ⋅ (π/180°)

θ = π/2

Using a calculator determine the solution for each equation, of two decimal places on the interval 0 ≤ x ≤ 2π

Example 11 :

3 sin x = sin x + 1

Solution :

3 sin x = sin x + 1

3 sin x - sin x = 1

2 sin x = 1

sin x = 1/2

x = sin^-1(1/2)

Since the value is positive for sin, the value of lies in the first and second quadrant.

x = π/6

x = 0.52

Value of x in the second quadrant :

x = π - π/6

x = 5π/6

x = 2.61

So, the values of x are 0.52 and 2.61

Example 12 :

sin 2x = 1/√2

Solution :

sin 2x = 1/√2

2x = sin^-1(1/√2)

2x = sin^-1(0.707)

Finding value of x lies in the first quadrant :

Using calculator, we get

2x = 0.7676

x = 0.7676/2

x = 0.3838

Finding the value of x lies in the second quadrant :

2x = 3.14 - 0.7676

2x = 2.3724

x = 2.3724 / 2

x = 1.1862

Multiple angles lies in first and second quadrant are,

3.14 + 0.3838 and 3.14 + 1.1862

3.5238 and 4.3262

Example 13 :

sin 3x = -√3/2

Solution :

sin 3x = -√3/2

3x = sin^-1(-√3/2)

Reference angle is π/3

3x = (π/3) - π

3x = -2π/3

3x = -2π/3 + 2π

3x = 4π/3

To get more values of x lies in 3rd quadrant :

3x = 4π/3 + 2nπ

x = 4π/9 + (2nπ/3)

When n = 0

x = 4π/9 

x = 1.39

To get more values of x lies in 4th quadrant :

3x = 2π - (π/3) + 2nπ

3x = (5π/3) + 2nπ

x = 5π/9 + (2nπ/3)

When n = 0

x = 5π/9

x = 1.74

So, the values of x are 

1.39, 1.74, 3.48, 3.83, 5.58, 5.93

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.