INVERSE FUNCTION

Let f be a one-one onto function from A to B.

Let y be an arbitrary element of B.

Then f being onto, there exists an element x in A such that 

f(x) = y

So, we may define a function, denoted as f^-1 as

f^-1 : B ---> A : f^-1(y) = x

if and only if f(x) = y.

The above function f^-1 is called the inverse of f.

A function is invertible, if and only if f is one-one onto. 

More clearly, one-one onto function will have an inverse function

You may be able to find f^-1 for any function f.

But, f^-1 will also be a function, only if f is one-one onto function.  

Remarks : 

If f is one-one onto, then f^-1 is also one-one onto. 

Illustration : 

If f : A ---> B, then

f^-1 : B---> A

Example 1 :

Find the inverse of the function f(x) = 2x + 3.

Solution :

f(x) = 2x + 3

Replace f(x) by y.

y = 2x + 3

Interchange x and y. 

x = 2y + 3

Solve for y.

x - 3 = 2y

y = (x - 3)/2

Replace y by f^-1(x).

f^-1(x) = (x - 3)/2

f^-1 (x)  =  (x - 3)/2

Example 2 :

Find the inverse of the function f(x) = x².

Solution :

Replace f(x) by y.

y = x²

Interchange x and y. 

x = y²

y² = x

Solve for y. Taking square root on both sides, 

y = ±√x

Replace y by f^-1(x).

f^-1(x) = ±√x

Example 3 :

Find the inverse of the function h(x) = log₁₀(x). 

Solution :

h(x) = log₁₀(x)

Replace h(x) by y.

y = log₁₀(x)

Interchange x and y. 

x = log₁₀(y)

Solve for y.

y = 10^x

Replace y by h^-1(x).

h^-1(x) = 10^x

Example 4 :

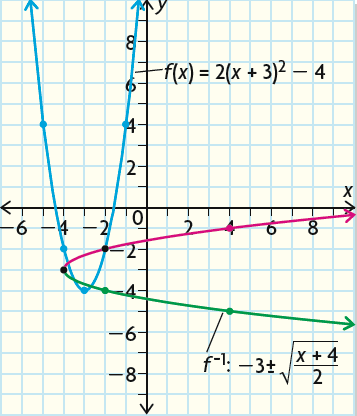
Find the inverse of the quadratic function and graph it. 

f(x) = 2(x + 3)² - 4

Solution :

Replace f(x) by y.

y = 2(x + 3)² - 4

Interchange x and y. 

x = 2(y + 3)² - 4

Solve for y. 

x + 4 = 2(y + 3)²

(x + 4)/2 = (y + 3)²

Take square root on both sides. 

±√[(x + 4)/2] = y + 3

±√[(x + 4)/2] - 3 = y

y = -3 ± √[(x + 4)/2]

Replace y by f^-1(x).

f^-1(x) = -3 ± √[(x + 4)/2]

Graphing the inverse of f(x) :

We can graph the original function by plotting the vertex (-3, -4). The parabola opens up, because a is positive.

And we get f(-2) = -2 and f(-1) = 4, which are also the same values of f(-4) and f(-5) respectively.

To graph f^-1(x), we have to take the coordinates of each point on the original graph and switch the x and y coordinates.

For example, (-1, 4) becomes (4, -1).

We have to do this because the input value becomes the output value in the inverse, and vice versa.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.