INTRODUCTION TO IRRATIONAL NUMBERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We all know that a number that is expressed in the form a/b is called as rational number.
Here both "a" and "b" are integers and also b ≠ 0.
Let us consider the decimal number that is given below.
0.21757575................
Here, after the decimal, we have the repeated pattern 75. This is the decimal number which is non terminating with repeated pattern.
So, this decimal number can be converted in to fraction. That is in the form a/b.
So, 0.21757575................ is rational.
Let us consider the decimal number which is non terminating and also it has no repeated pattern.
2.17526325890748......................
A non terminating decimal which does not have repeated pattern is called as irrational number.
To have better understanding of irrational numbers, let us know the difference between rational and irrational numbers.
Difference between Rational and Irrational Numbers
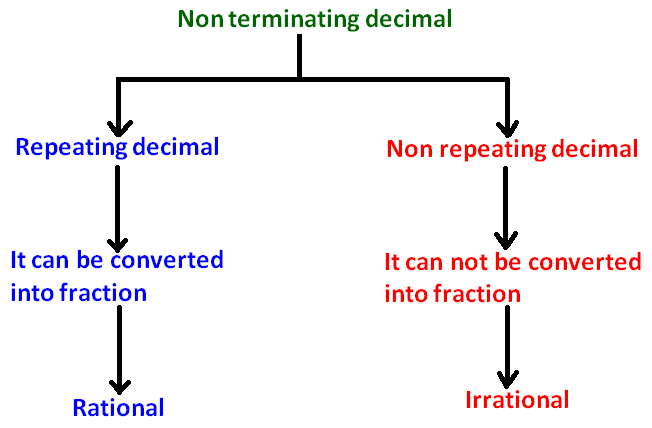
Example :
Rational :
1.2626262626.............(Repeated pattern is 26)
Irrational :
1.4142135623............(No repeated pattern)
More clearly,
A non terminating decimal which has repeated pattern is called as rational number.
Because, the non terminating decimal which has repeated pattern can be converted into fraction.
A non terminating decimal which does not have repeated pattern is called as irrational number.
Because, the non terminating decimal which does not have repeated pattern can not be converted into fraction.
To have better understanding on the difference between rational and irrational numbers, let us come to know about rational numbers and irrational numbers more clearly.
What are rational and irrational numbers ?
First let us come to know, what is rational number. Because, once we understand rational number, we can easily understand irrational number.
A rational number has to be in the form as given below.
Rational Numbers

So, any number in the form of fraction can be treated as rational number.
Examples of Rational Number :
5, 2.3, 0.02, 5/6
Because all these numbers can be written as fractions.
5 = 5/1
2.3 = 23/10
0.02 = 2/100 = 1/50
5/6 (This is already a fraction)
Apart from the above examples, sometimes we will have recurring decimals like 1.262626..........
1.262626........ is a non terminating recurring decimal.
All these recurring decimals can be converted to fractions and they are also rational numbers.
Irrational Numbers
A number which can not be converted into fraction is called as irrational numbers.
Examples of Irrational Number :

All the above non terminating numbers can not be converted into fractions.
Because, they do not have repeated patterns.
When we are trying to find square of a number which is not a perfect square, we get this non repeating non terminating decimal.
And these non recurring decimals can never be converted to fractions and they are called as irrational numbers.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations