INTRODUCTION TO FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The coordinate plane is formed by the intersection of two perpendicular number lines called axes . The point of intersection, called the origin , is at 0 on each number line. The horizontal number line is called the x-axis , and the vertical number line is called the y-axis .
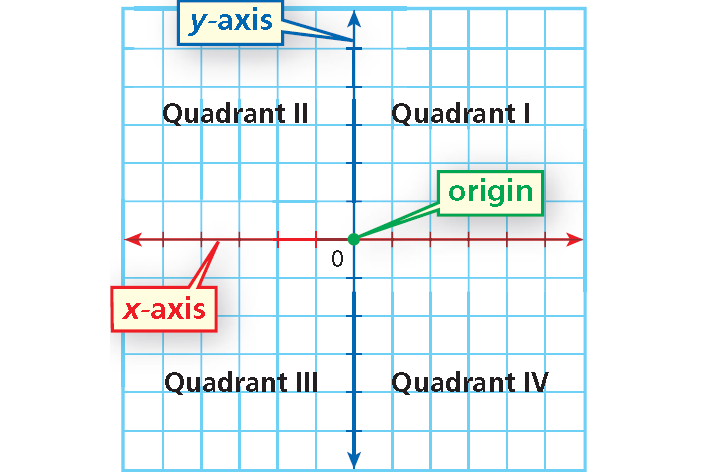
Points on the coordinate plane are described using ordered pairs. An ordered pair consists of an x-coordinate and a y-coordinate and is written (x, y). Points are often named by a capital letter.
Graphing Points in the Coordinate Plane
Example 1 :
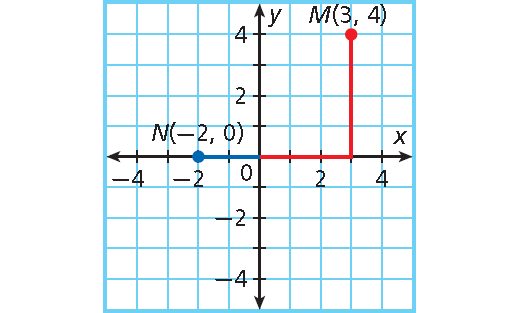
Graph each point :
M(3, 4), N(-2, 0)
Solution :
|
M(3, 4) |
Start at the origin. Move 3 units right and 4 units up. |
|
N(-2, 0) |
Start at the origin. Move 2 units left. |
Locating Points in the Coordinate Plane
Example 2 :
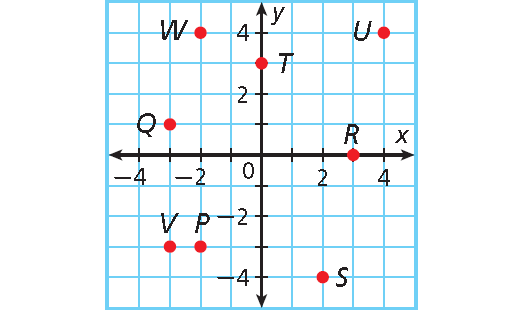
Name the quadrant in which each point lies.
Solution :
P -----> Quadrant III
Q -----> Quadrant II
R -----> No Quadrant (x-axis)
S -----> Quadrant IV
T -----> Quadrant I
U -----> Quadrant I
V -----> Quadrant III
W -----> Quadrant II
Function
An equation that contains two variables can be used as a rule to generate ordered pairs. When you substitute a value for x, you generate a value for y. The value substituted for x is called the input , and the value generated for y is called the output .
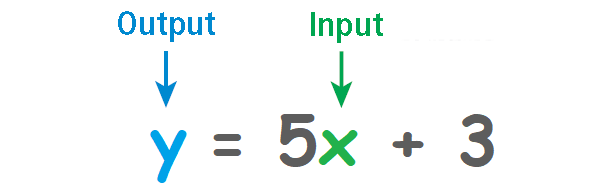
In a function, the value of y (the output) is determined by the value of x (the input). All of the equations in this lesson represent functions.
Solving Application Problem
Example 3 :
A caricature artist charges his clients a $5 setup fee plus $10 for every person in a picture. Write a rule for the artist’s fee. Write ordered pairs for the artist’s fee when there are 1, 2, 3, and 4 people in the picture.
Solution :
Let y represent the artist’s fee and x represent the number of people in a picture.
Artist’s fee is $5 plus $10 for each person.
y = 5 + 10 · x
y = 5 + 10x
No. of People in Picture
Rule
Fee
Ordered Pair
x (input)
y = 5 + 10x
y (output)
(x , y)
1
2
3
4
y = 5 + 10(1)
y = 5 + 10(2)
y = 5 + 10(3)
y = 5 + 10(4)
15
25
35
45
(1 , 15)
(2 , 25)
(3 , 35)
(4 , 45)
Note :
When ordered pairs generated by a function are graphed, they may create a pattern.
Generating and Graphing Ordered Pairs
Generate ordered pairs for each function using the given values for x. Graph the ordered pairs and describe the pattern.
Example 4 :
y = 4x - 3 ; x = -1, 0, 1, 2
Solution :
Input
x
Output
y
Ordered Pair
(x, y)
-1
0
1
2
4(-1) - 3 = -7
4(0) - 3 = -3
4(1) - 3 = 1
4(2) - 3 = 5
(-1 , -7)
(0 , -3)
(1 , 1)
(2 , 5)
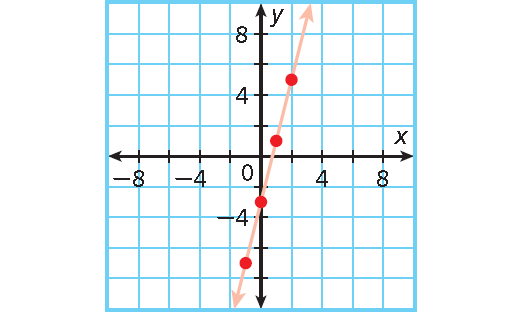
The points form a straight line.
Example 5 :
y = 2x2 + 1 ; x = -2, -1, 0, 1, 2
Solution :
Input
x
Output
y
Ordered Pair
(x, y)
-2
2(-2)2 + 1 = 9
(-2 , 9)
-1
2(-1)2 + 1 = 3
(-1 , 3)
0
2(0)2 + 1 = 1
(0 , 1)
1
2(1)2 + 1 = 3
(1 , 3)
2
2(2)2 + 1 = 9
(1 , 9)
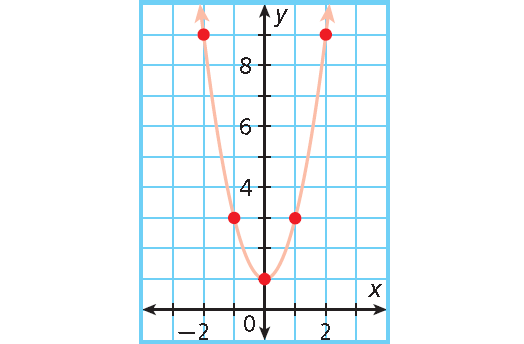
The points form a U shape.
Example 6 :
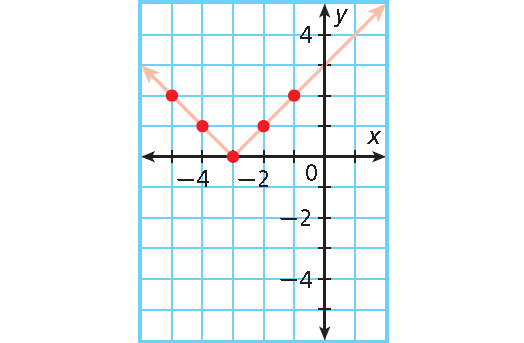
y = |x + 3| ; x = -5, -4, -3, -2, -1
Solution :
Input
x
Output
y
Ordered Pair
(x, y)
-5
-4
-3
-2
-1
|-5 + 3| = |-2| = 2
|-4 + 3| = |-1| = 1
|-3 + 3| = |0| = 0
|-2 + 3| = |1| = 1
|-1 + 3| = |2| = 2
(-5 , 2)
(-4 , 1)
(-3 , 0)
(-2 , 1)
(-1 , 2)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

