INTERPRETING THE UNIT RATE AS SLOPE WORKSHEET

Problem 1 :

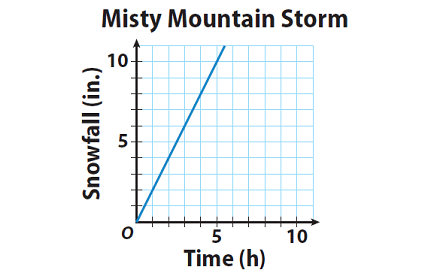
A storm is raging on Misty Mountain. The graph shows the constant rate of change of the snow level on the mountain.

Questions :

A.  Find the slope of the graph using the points (1, 2) and (5, 10). Remember that the slope is the constant rate of change.

B. Find the unit rate of snowfall in inches per hour. Explain your method.

C. Compare the slope of the graph and the unit rate of change in the snow level. What do you notice ?

D. Which unique point on this graph can represent the slope of the graph and the unit rate of change in the snow level ? Explain how you found the point.

Problem 2 :

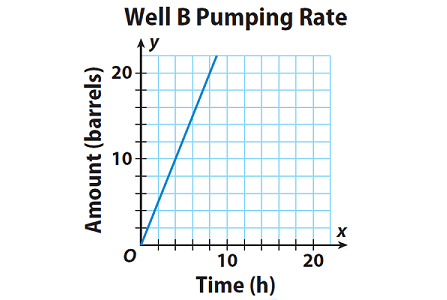
The equation y = 2.75x represents the rate, in barrels per hour, that oil is pumped from Well A. The graph represents the rate that oil is pumped from Well B. Which well pumped oil at a faster rate ?

1. Answer :

A.  Find the slope of the graph using the points (1, 2) and (5, 10). Remember that the slope is the constant rate of change.

Change in y-value / Change in x-value :

=  (10-2)/(5-1)

=  8 / 4

=  2

B. Find the unit rate of snowfall in inches per hour. Explain your method.

2 inches per hour; Sample answer : The point (1, 2) is on the line, and represents 2 inches snowfall in 1 hour.

C.  Compare the slope of the graph and the unit rate of change in the snow level. What do you notice ?

They are the same.

D.  Which unique point on this graph can represent the slope of the graph and the unit rate of change in the snow level ? Explain how you found the point.

(1, 2) ; Sample answer : the unit rate is the amount of snow in 1 hour. So I found the point with an x-coordinate of 1. That point is (1, 2), which, along with another point on the graph, gives 2 as the slope.

2. Answer :

Step 1 :

Use the equation y = 2.75x to make a table for Well A’s pumping rate, in barrels per hour.

Step 2 :

Use the table to find the slope of the graph of Well A.

Slope  =  Unit rate 

Slope  =  (5.5 - 2.75) / (2 - 1) 

Slope  =  2.75 / 1

Slope  =  2.75 barrels/hour.

Step 3 :

Use the graph to find the slope of the graph of Well B.

Slope  =  Unit rate 

Slope  =  rise / run 

Slope  =  10 / 4

Slope  =  2.5 barrels/hour.

Step 4 :

Compare the unit rates.

2.75 > 2.5

So Well A’s rate, 2.75 barrels/hour, is faster.

Reflect :

Describe the relationships among the slope of the graph of Well A’s rate, the equation representing Well A’s rate, and the constant of proportionality

The slope and the constant of proportionality equal the value 2.75 in the equation y = 2.75x.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.