INTERPRETING LINEAR MODELS WORKSHEET

Problem 1 :

For a lemonade stand, the total cost c, in dollars of selling n cups of lemonade is given by c = 100 + 1.5n. What is the best interpretation of the number 100 in this equation?

A) The cost of each cup of lemonade.

B) The number of cups of lemonade sold on the first day.

C) The initial cost of setting up the lemonade stand.

D) The maximum total cost of running the lemonade stand.

Problem 2 :

The number of books in the warehouse can be found using the expression 4000 + 100bd, where 'b' is the number of boxes of books the warehouse receives each day over a period of 'd' days. What is the best interpretation of the number 100 in the expression?

A) The number of books in each box.

B) The number of books received each day.

C) The number of boxes received that contain boxes.

D) The number of days it takes to receive each box.

Problem 3 :

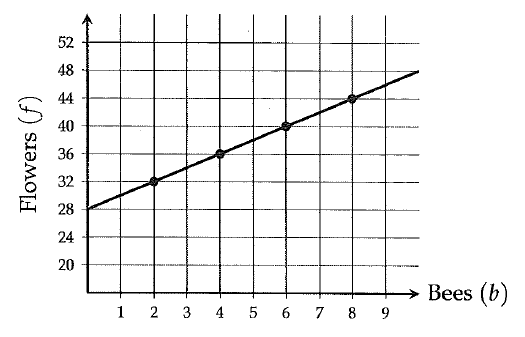
A botanist uses the graph above to show the number of flowers 'f' that blossom in a garden with 'b' bees.

(i) What is the meaning of f-intercept?

(ii) Write a linear function which describes the relationship between 'f' and 'b' and also interpret it.

Problem 4 :

A food manufacturer fills containers of seasoning with various spices, pepper and salt. The amount of pepper 'p', in milligrams, used in the seasoning can be modeled by the equation 

p = (10 + 3s)/4

where 's' is the amount of salt, in milligrams, in the seasoning. According to the model, how many milligrams of pepper are added for every 1 milligram increase in the amount of salt?

Problem 5 :

The total amount of water w, in gallons, left in a tank can be modeled by the equation w = 300 - 5t, where 't' is the number of hours since the tank started leaking. Which of the following is the best interpretation of the number 5 in the equation?

A) The tank is empty after 5 hours.

B) The tank loses 5 gallons of water each hour.

C) The tank continues to lose water until 5 gallons are left.

D) Each hour, the tank loses 5 less gallons of water than it did the previous hour.

Problem 6 :

A manufacturer produces 80 units of a particular product at a cost of $ 220000 and 125 units at a cost of $ 287500. Assuming the cost curve to be linear, find the cost of 95 units.

Problem 7 :

Loretta works as a cook in northern Saskatchewan. She is paid $14 an hour plus $200 a week for working in a remote location. Let t represent the time in hours Loretta works each week and let d represent her weekly pay in dollars.

a) Write an equation that relates d and t.

b) What will Loretta’s weekly earnings be when she works 35 h?

c) For how many hours did Loretta work when her weekly pay was $718?

d) Can Loretta earn exactly $600 in one week? Explain.

1. Solution :

In c = 100 + 1.5n, 'c' stands for the total cost of lemonade stand.

The number 100 in the equation is not influenced by the number of cups 'n'.

Moreover, when n = 0,

c = 100 + 1.5(0)

c = 100

So, 100 is the initial value of 'c' or the initial cost of setting up the lemonade stand.

The correct answer choice is (C).

2. Solution :

In 4000 + 100bd,

b ----> number of boxes

d ----> number of days

bd = total number of boxes received in 'd' days

Since the given expression represents the total number of books in the warehouse, the number 100 must be the number of books in each box.

The correct answer choice is (A).

3. Solution :

Part (i) :

f ---> number of flowers

b ----> number of bees

In the graph shown above, f-intercept is the value of 'f' when b = 0.

So, f-intercept is the number of flowers that blossom in the garden without any bees.

Part (ii) :

In the graph shown above, f-intercept is 28.

The line goes up 4 units for every 2 units to the right. So, the slope is

= 4/2

= 2

The linear function describes the relationship between 'f' and 'b' :

f = 28 + 2b

Interpreting f = 28 + b :

If b = o,

f = 28 + 2(0)

f = 28

When there is no bee in the garden, the number of flowers that blossom in the garden is 28.

If b = 1,

f = 28 + 2(1)

f = 30

If b = 2,

f = 28 + 2(2)

f = 32

Clearly, if there is an increase 1 bee, there is an increase of 2 flowers in the garden.

4. Solution :

Write the given equation in the form y = mx + b.

p = (10 + 3s)/4

p = 10/4 + 3s/4

p = 2.5 + (3/4)s

The slope is 3/4 (positive value). 

There is an increase of 3 milligrams of pepper for every 4 milligram increase of salt.

4 milligrams of salt ---> 3 milligrams of pepper

1 milligram of salt ----> 3/4 or 0.75 milligrams of pepper

Therefore, 0.75 milligrams of pepper are added for every 1 milligram increase in the amount of salt.

5. Solution :

In w = 300 - 5t, the slope is -5 (negative value).

-5 = -5/1

There is a decrease of 5 units of 'w' for every 1 unit increase of 't'.

That is, the tank loses 5 gallons of water each hour.

The correct answer choice is (B).

6. Solution :

From the information given, it is clear that the cost curve is linear.

The function which best fits the given information is a linear-cost function.

y = mx + b

where 'y' is the total cost and 'x' is the number of units.

We have to find the value of 'y' for x = 95.

From the information given, we have

x = 80  and  y = 220000

x = 75  and  y = 287500

When we substitute the above values of 'x' and 'y' in

y = mx + b,

we get 

220000 = 80m + b

287500 = 75m + b

Solving the above equations,

m = 1500  and  b = 100000

Now, the cost function is

y = 1500x + 100000

Substitute x = 95.

y = 1500(95) + 100000

= 142500 + 100000

= 242500

So, the cost of 95 units is $242,500.

7. Solution :

Part (a) :

d = 14t + 200

Part (b) :

Substitute t = 35 in the equation in part (a) and evaluate d..

d = 14(35) + 200

d = 490 + 200

d = 690

When Loretta works 35 h, her weekly earnings will be $690.

Part (c) :

Substitute d = 718 in the equation in part (a) and solve for t..

718 = 14t + 200

Subtract 200 from both sides.

518 = 14t

Divide both sides by 14.

37 = t

When Loretta's weekly pay was $718, she worked for 37 hours.

Part (d) :

Substitute d = 600 in the equation in part (a) and solve for t.

600 = 14t + 200

Subtract 200 from both sides.

400 = 14t

Divide both sides by 14.

28.57 ≈ t

Since the number of hours t is not an integer, Loretta can not earn exactly $600 in one week.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.