INTERPRETING GRAPHS
About "Interpreting graphs"
Interpreting graphs :
In this section, we are going to see, how to describe a relationship between two variables x and y by interpreting the graph.
Interpreting graphs - Examples
Example 1 :
A square tile has a side length of x inches. The equation aaa y = x² gives the area of the tile in square inches. Determine whether the rate of change between the side length and area of a square is constant using the graph. And also describe whether the relationship between the two variables is linear.
Solution :
Step 1 :
Choose several values for the input x. Plug these values for x in the equation to find the output y.
x
1
2
3
4
x²
1²
2²
3²
4²
y
1
4
9
16
(x, y)
(1, 1)
(2, 4)
(3, 9)
(4, 16)
Step 2 :
Graph the ordered pairs. Then draw a line through the points to represent the solutions of the function.
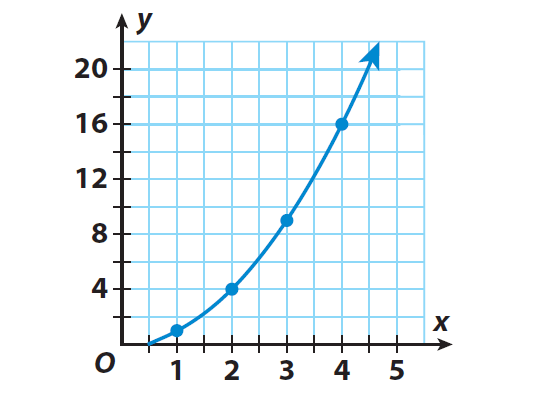
Step 3 :
Describe the relationship between x and y.
The graph is not a straight line. So the rate of change between the side length and area of a square is not constant.
Only a straight line graph will represent a linear relationship. Since the graph is not a straight line, the relationship between the two variables x and y is non linear.
Example 2 :
The temperature of a fish tank was 82 °F and decreased steadily 2 °F every hour. The equation y = -2x + 82 gives the temperature y after x hours. Determine whether the rate of change between the time and temperature is constant. And also describe whether the relationship between the two variables is linear.
Solution :
Step 1 :
Choose several values for the input x. Plug these values for x in the equation to find the output y.
x
0
1
2
3
4
5
-2x + 82
-2(0) + 82
-2(1) + 82
-2(2) + 82
-2(3) + 82
-2(4) + 82
-2(5) + 82
y
82
80
78
76
74
72
(x, y)
(0, 82)
(1, 80)
(2, 78)
(3, 76)
(4, 74)
(5, 72)
Step 2 :
Graph the ordered pairs. Then draw a line through the points to represent the solutions of the function.
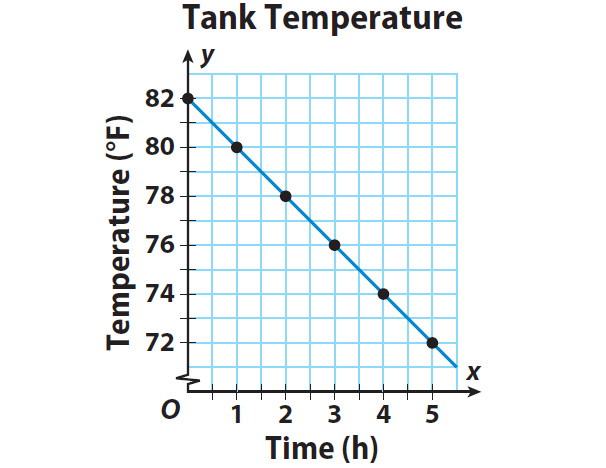
Step 3 :
Since the graph is a straight line, the rate of change between the time and temperature is constant.
Since the rate of change is constant and the graph is a straight line, the relationship between the two variables x and y is linear.
After having gone through the stuff given above, we hope that the students would have understood "Interpreting graphs".
Apart from the stuff given above, if you want to know more about "Interpreting graphs", please click here
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
