INTERPRET QUOTIENTS OF RATIONAL NUMBERS BY DESCRIBING REAL-WORLD CONTEXTS

In mathematics, a rational number is any number that can be expressed in the form p/q where "q" is not equal to zero.

The quotient of the rational number p/q is nothing but the result that we get when we divide "p" by "q". 

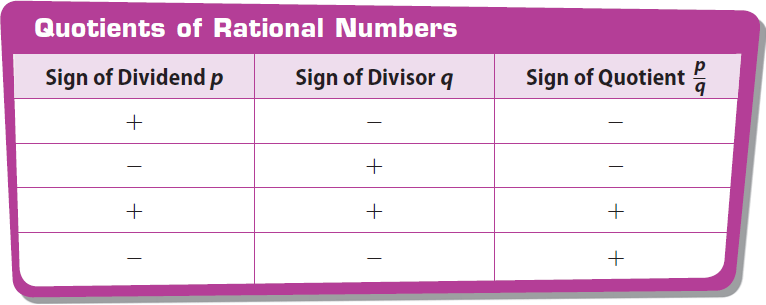
The rules for the sign of quotient are summarized below.

Let p and q be rational numbers.

Example 1 : 

A diver needs to descend to a depth of 100 feet below sea level. She wants to do it in 5 equal descents. How far should she travel in each descent ?

Solution :

To find how far she should travel in each descent, we have to divide 100 by 5. 

Step 1 :

Take the reciprocal of the divisor 5.

5 ---- reciprocal ----> 1/5

Step 2 : 

Multiply 100 by 1/5

(100) x (1/5)  

Step 3 : Simplify

(20) x (1/1)

Step 4 : Multiply 

(20) x (1/1)  =  20    

So, she should travel 20 feet in each descent.

Example 2 : 

Over 5 months, Carlos wrote 5 checks for a total of $323.75 to pay for his cable TV service. His cable bill is the same amount each month. What was the change in Carlos’s bank account each month to pay for cable?

Solution :

Step 1 :

Use a negative number to represent the withdrawal from his account each month

Step 2 : 

Find -323.75 / 5 

Step 3 : 

Determine the sign of the quotient.

The quotient will be negative because the signs are different.

Step 4 :

Divide. 

-323.75 / 5  =  -64.75 

So, Carlos withdrew $64.75 each month to pay for cable TV.

Example 3 : 

Maya wants to divide a 3/4 -pound box of trail mix into small bags. Each bag will hold 1/12 pound of trail mix. How many bags of trail mix can Maya fill ?

Solution : 

Step 1 : 

To get answer for the above question, we have to divide 3/4 by 1/12.

That is, we have to find the value of (3/4) / (1/12).

Step 2 : 

Determine the sign of the quotient.

The quotient will be positive, because the signs of both numerator (3/4) and denominator (1/12) are same. 

Step 3 : 

Write the complex fraction as division :

(3/4) / (1/12)  =  (3/4) ÷ (1/12)

Step 4 : 

Rewrite the above division as multiplication by taking the reciprocal of the second fraction. 

(3/4) ÷ (1/12)  =  (3/4) x (12/1)

Step 5 : 

Simplify

(3/4) x (12/1)  =  (3/1) x (3/1)

(3/4) x (12/1)  =  9

So, Maya can fill 9 bags of trail mix.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.