INTERIOR ANGLES OF A QUADRILATERAL WORKSHEET

Problem 1 :

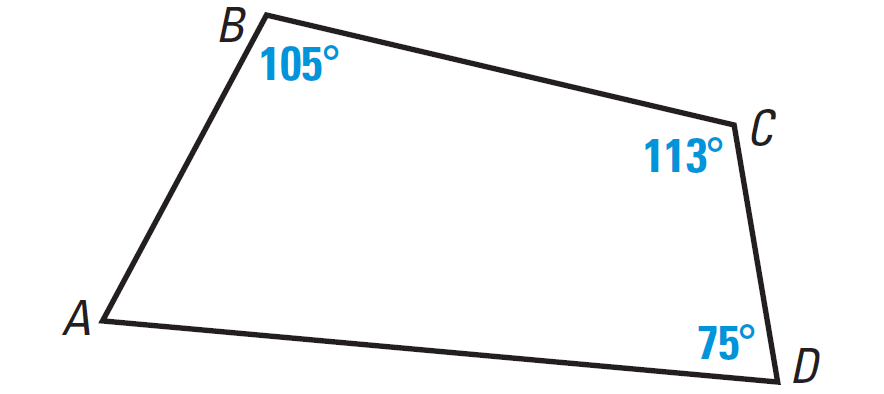
In the diagram shown below, find m∠A. 

Problem 2 :

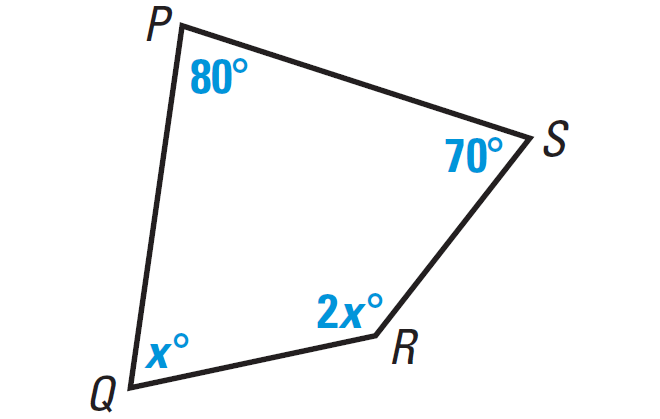
In the diagram shown below, find the value of x. 

Problem 3 :

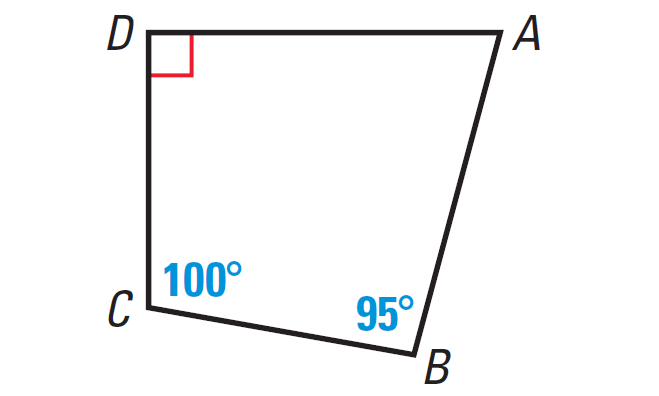
In the diagram shown below, find m∠A. 

Problem 4 :

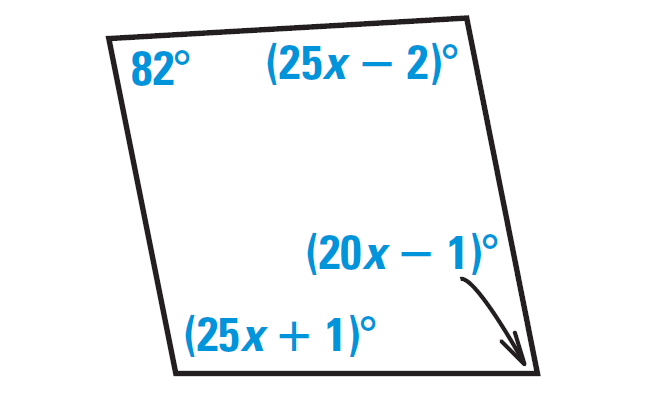
In the diagram shown below, find the value of x. 

Problem 5 :

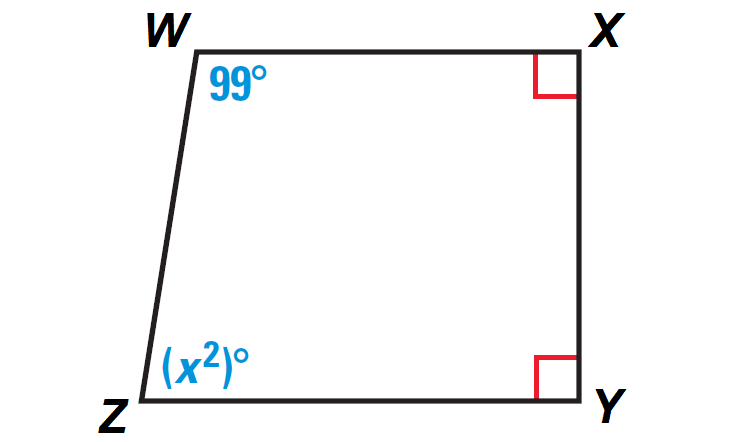
In the diagram shown below, find the value of x.

Problem 6 :

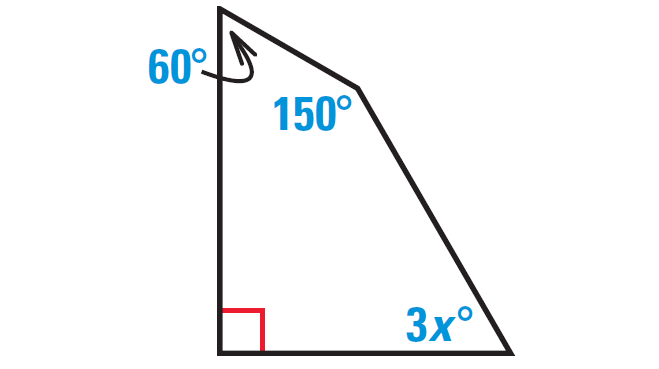
In the diagram shown below, find the value of x. 

Problem 7 :

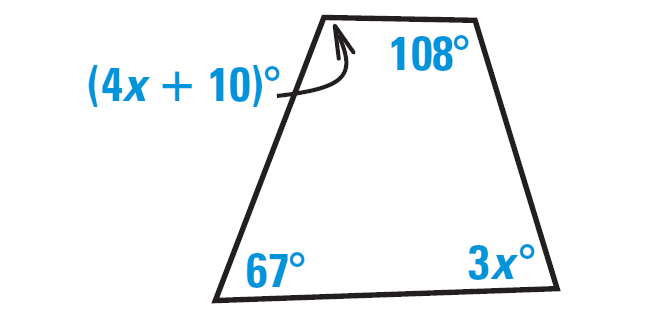
In the diagram shown below, find the value of x.

Problem 8 :

In the diagram shown below, find the values of x and y. 

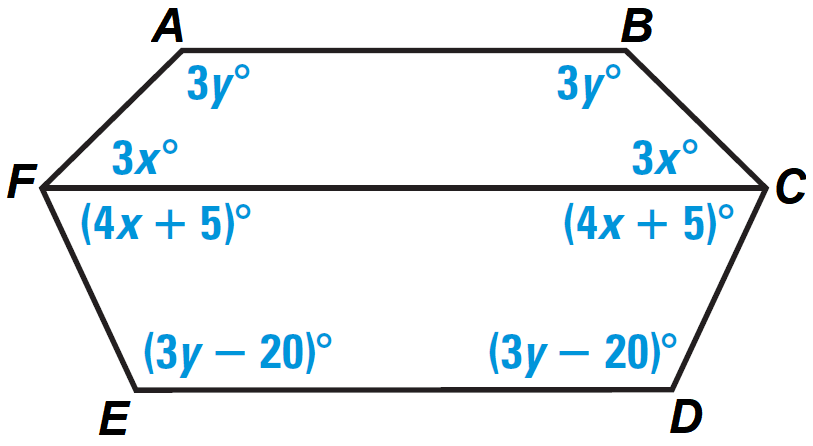
Answers

1. Answer :

Because the figure ABCD is a closed figure and it is covered by four segments, it is quadrilateral.    

By Internal Angles of a Quadrilateral Theorem, we have 

m∠A  +  m∠B  +  m∠C  +  m∠D  =  360°

Substitute m∠B = 105°, m∠C = 113°, m∠D = 75°.

m∠A  +  105°  +  113°  +  75°  =  360°

Simplify. 

m∠A  +  293°  =  360°

Subtract 293° from both sides. 

m∠A  =  67°

2. Answer :

Because the figure PQRS is a closed figure and it is covered by four segments, it is quadrilateral.    

By Internal Angles of a Quadrilateral Theorem, we have 

m∠P  +  m∠Q  +  m∠R  +  m∠S  =  360°

Substitute m∠P = 80°, m∠Q = x°, m∠R = 2x°, m∠S = 70°.

80°  +  x°  +  2x°  +  70°  =  360°

Simplify. 

3x°  +  150°  =  360°

Subtract 150° from both sides. 

3x°  =  210°

3x  =  210

Divide both sides by 3. 

x  =  70

3. Answer :

Because the figure ABCD is a closed figure and it is covered by four segments, it is quadrilateral.

In quadrilateral ABCD above, angle A is a right angle.

So, we have

m∠D  =  90°

By Internal Angles of a Quadrilateral Theorem, we have 

m∠A  +  m∠B  +  m∠C  +  m∠D  =  360°

Substitute m∠B = 95°, m∠C = 100°, m∠D = 90°.

m∠A  +  95°  +  100°  +  90°  =  360°

Simplify. 

m∠A  +  285°  =  360°

Subtract 285° from both sides. 

m∠A  =  75°

4. Answer :

Because the figure shown above is a closed figure and it is covered by four segments, it is quadrilateral.

By Internal Angles of a Quadrilateral Theorem, 

"The sum of the measures of the interior angles of a quadrilateral is 360°"

So, we have

82°  +  (25x - 2)°  +  (20x - 1)°  +  (25x + 1)°  =  360°

82  +  25x - 2  +  20x - 1  +  25x + 1  =  360

Simplify. 

70x + 80  =  360

Subtract 80 from both sides. 

70x  =  280

Divide both sides by 70.

x  =  4

5. Answer :

Because the figure WXYZ is a closed figure and it is covered by four segments, it is quadrilateral.

In quadrilateral WXYZ above, angles X and Y are right angles.

So, we have

m∠X  =  90°

m∠Y  =  90°

By Internal Angles of a Quadrilateral Theorem, 

m∠W  +  m∠X  +  m∠Y  +  m∠Z  =  360°

Substitute m∠W = 99°, m∠X = 90°, m∠Y = 90°, m∠Z = (x²)°.

99°  +  90°  +  90°  +  (x²)°  =  360°

99  +  90  +  90  +  x²  =  360

Simplify. 

279  +  x²  =  360

Subtract 279 from both sides. 

x²  =  81

x²  =  9²

x  =  9

6. Answer :

Because the figure shown above is a closed figure and it is covered by four segments, it is quadrilateral.

In the quadrilateral above, one of the angles marked in red color is right angle. 

By Internal Angles of a Quadrilateral Theorem, 

"The sum of the measures of the interior angles of a quadrilateral is 360°"

So, we have

60°  +  150°  +  3x°  +  90°  =  360°

60  +  150  +  3x  +  90  =  360

Simplify. 

3x  +  300  =  360

Subtract 300 from both sides. 

3x  =  60

Divide both sides by 3. 

x  =  20

7. Answer :

Because the figure shown above is a closed figure and it is covered by four segments, it is quadrilateral.

By Internal Angles of a Quadrilateral Theorem, 

"The sum of the measures of the interior angles of a quadrilateral is 360°"

So, we have

(4x + 10)°  +  108°  +  3x°  +  67°  =  360°

4x + 10  +  108  +  3x  +  67  =  360

Simplify. 

7x + 185  =  360

Subtract 185 from both sides. 

7x  =  175

Divide both sides by 7.

x  =  25

8. Answer :

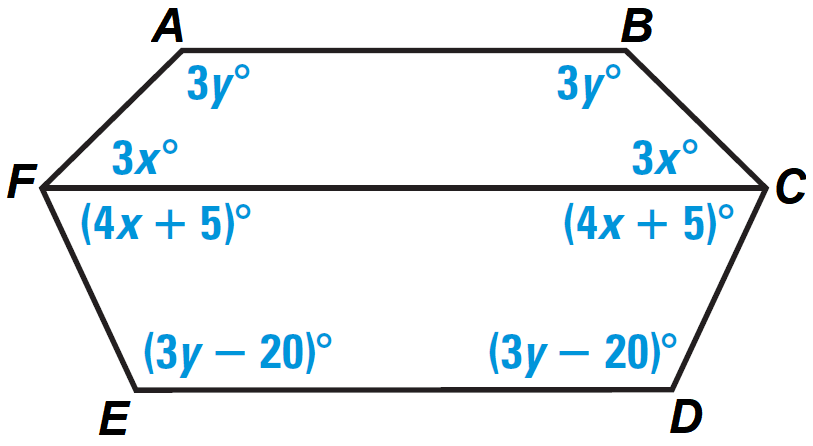
In the diagram above, figure ABCF is a closed figure and it is covered by four segments, it is quadrilateral.

In quadrilateral ABCF, by Internal Angles of a Quadrilateral Theorem, 

m∠A  +  m∠B  +  m∠C  +  m∠F  =  360°

3y°  +  3y°  +  3x°  +  3x°  =  360°

Simplify.

6y°  +  6x°  =  360°

6x  +  6y  =  360

Divide both sides by 6.

x  +  y  =  60 -------(1)

In the diagram above, figure FCDE is a closed figure and it is covered by four segments, it is quadrilateral.

In quadrilateral FCDE, by Internal Angles of a Quadrilateral Theorem,

m∠F  +  m∠C  +  m∠D  +  m∠E  =  360°

(4x + 5)°  +  (4x + 5)°  +  (3y - 20)°  +  (3y - 20)°  =  360°

4x + 5  +  4x + 5  +  3y - 20  +  3y - 20  =  360

Simplify.

8x  +  6y  -  30  =  360

8x  +  6y  =  390

Divide both sides by 2.

4x  +  3y  =  195 -------(2)

Solving (1) and (2), we get

x  =  15

y  =  45

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.