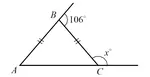
INTERIOR AND EXTERIOR ANGLES OF A POLYGON
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
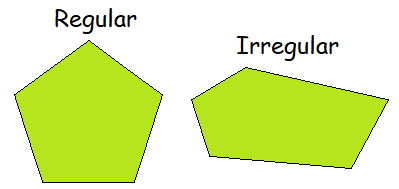
Regular Polygon :
A regular polygon has sides of equal length, and all its interior and exterior angles are of same measure.
Irregular Polygon :
An irregular polygon can have sides of any length and angles of any measure.
Example :
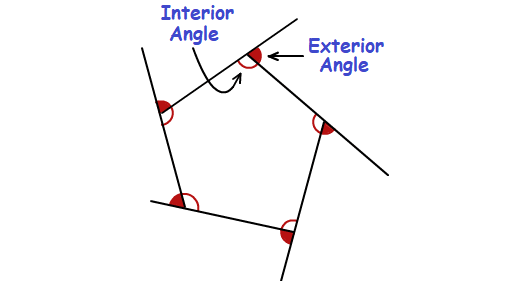
Interior and Exterior Angles of a Polygon
Interior Angle :
An interior angle of a polygon is an angle inside the polygon at each of its vertices.
Exterior Angle :
An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side.
More clearly,
Points to Remember
(i) If a polygon has "n" number of sides, then it would have "n" number of vertices, "n" number of interior angles and "n" number of exterior angles.
(ii) In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.
(iii) In any polygon, the sum of all exterior angles is 360°.
Example 1 :
What is the sum of the exterior angles of an octagon ?
Solution :
In any polygon, the sum of all exterior angles is 360°.
So, the sum of the exterior angles of an octagon is also 360°.
Example 2 :
What is the measure of one exterior angle of a regular decagon (ten-sided polygon) ?
Solution :
In any polygon, the sum of all exterior angles is 360°.
The given decagon is a regular polygon.
So, all its exterior angles are of same measure.
Because decagon is a ten-sided polygon, the measure of each exterior angle is
= 360°/10
= 36°
Hence, the measure of each exterior exterior angle of a regular decagon is 36°.
Example 3 :
What is the measure of each interior angle of a regular nonagon (nine-sided polygon) ?
Solution :
In any polygon, the sum of all exterior angles is 360°.
The given nonagon is a regular polygon.
So, all its exterior angles are of same measure.
Because nonagon is a nine-sided polygon, the measure of each exterior angle is
= 360°/9
= 40°
The measure of each exterior exterior angle of a regular nonagon is 40°.
In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.
That is,
Interior angle + Exterior Angle = 180°
Interior angle + 40° = 180°
Interior angle = 140°
Hence, the measure of each exterior exterior angle of a regular nonagon is 140°.
Example 4 :
One exterior angle of a regular polygon is 20°. How many sides does it have ?
Solution :
Let the given regular polygon has "n" number of sides.
The sum of all exterior angles of a polygon with "n" sides is
= No. of sides ⋅ Measure of each exterior angle
= n ⋅ 20° ------(1)
In any polygon, the sum of all exterior angles is
= 360° ------(2)
From (1) and (2), we have
n ⋅ 20° = 360°
n ⋅ 20 = 360
Divide both sides by 20.
n = 18
Hence, the regular polygon has 18 sides.
Example 5 :
One interior angle of a regular polygon is 165.6°. How many sides does it have ?
Solution :
Let the given regular polygon has "x" number of sides.
In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.
That is,
Interior angle + Exterior Angle = 180°
165.6° + Exterior Angle = 180°
Exterior angle = 14.4°
So, the measure of each exterior angle is 14.4°
The sum of all exterior angles of a polygon with "n" sides is
= No. of sides ⋅ Measure of each exterior angle
= x ⋅ 14.4° ------(1)
In any polygon, the sum of all exterior angles is
= 360° ------(2)
From (1) and (2), we have
x ⋅ 14.4° = 360°
x ⋅ 14.4 = 360
Divide both sides by 14.4
x = 25
Hence, the regular polygon has 25 sides.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 29)
Mar 01, 26 07:26 PM
Digital SAT Math Problems and Solutions (Part - 29) -
Digital SAT Math Problems and Solutions (Part - 28)
Mar 01, 26 06:25 PM
Digital SAT Math Problems and Solutions (Part - 28) -
Digital SAT Math Problems and Solutions (Part -27)
Feb 28, 26 07:46 PM
Digital SAT Math Problems and Solutions (Part -27)