INTERCEPTING A DIAMETER WORKSHEET

Problem 1 : 

In the diagram shown below, find m∠BAC.

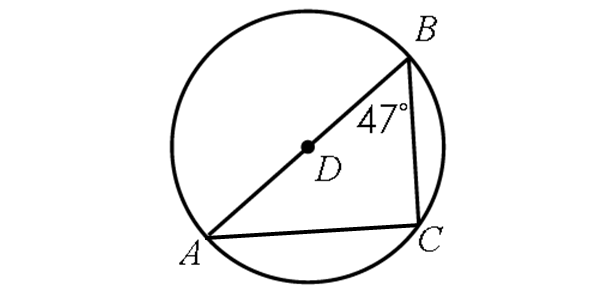
Problem 2 : 

In the diagram shown below, m∠QPR = 30°, find m∠PRQ.

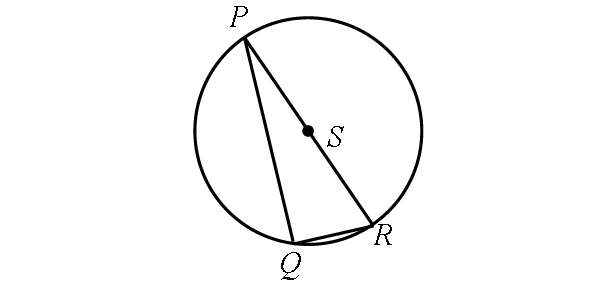
Problem 3 : 

Solve for x.

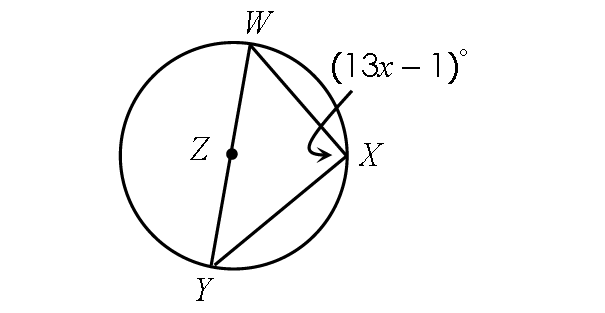
Problem 4 : 

Find m∠arc EF. 

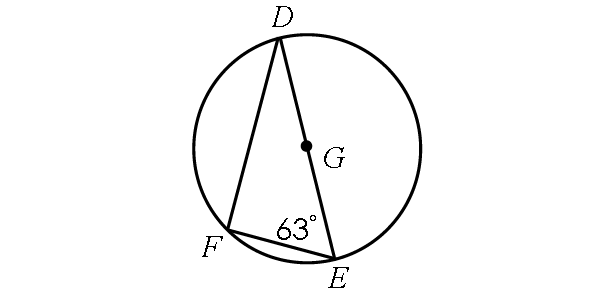
Problem 5 : 

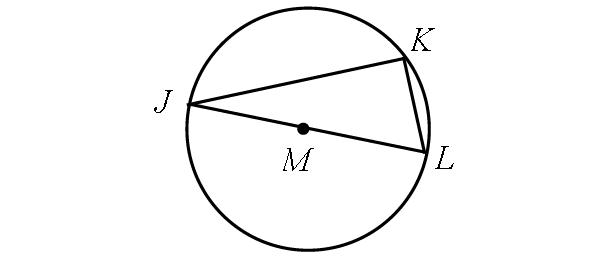
If m∠KJL = (3x + 2)° and m∠KLJ = (7x - 32)°, find m∠arc KL. 

Problem 6 : 

Solve for x.

Detailed Answer Key

Problem 1 : 

In the diagram shown below, find m∠BAC.

Solution  : 

In the diagram shown above, the inscribed angle m∠BCA intercepts the diameter AB. 

Then, 

m∠BCA  =  90°

In Δ ABC, 

m∠A + m∠B + m∠C  =  180°

Substitute m∠B  =  47° and m∠C  =  90°.

m∠A + 47° + 90°  =  180°

m∠A + 137°  =  180°

Subtract 137° from each side. 

m∠A  =  43°

So, 

m∠BAC  =  43°

Problem 2 : 

In the diagram shown below, m∠QPR = 30°, find m∠PRQ.

Solution  : 

In the diagram shown above, the inscribed angle m∠PQR intercepts the diameter PR. 

Then, 

m∠PQR  =  90°

In Δ PQR, 

m∠P + m∠Q + m∠R  =  180°

Substitute m∠P  =  30° and m∠Q  =  90°.

30° + 90° + m∠R  =  180°

120° + m∠R  =  180°

Subtract 120° from each side. 

m∠R  =  60°

So, 

m∠PRQ  =  60°

Problem 3 : 

Solve for x.

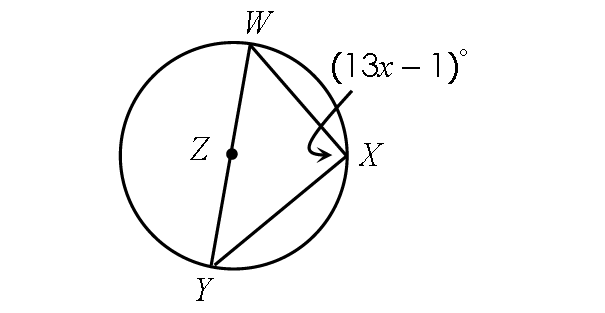
Solution  : 

In the diagram shown above, the inscribed angle m∠WXY intercepts the diameter WY. 

Then, 

m∠WXY  =  90°

(13x - 1)°  =  90°

13x - 1  =  90

Add 1 to each side. 

13x  =  91

Divide each side 13.

x  =  7

Problem 4 : 

Find m∠arc EF. 

Solution  : 

In the diagram shown above, the inscribed angle m∠DFE intercepts the diameter DE. 

Then, 

m∠DFE  =  90°

In Δ DEF, 

m∠D + m∠E + m∠F  =  180°

Substitute. 

m∠D + 63° + 90°  =  180°

m∠D + 153°  =  180°

Subtract 153° from each side. 

m∠D  =  27°

m∠EDF  =  27°

By Inscribed Angle Theorem, 

m∠arc EF  =  2 ⋅ m∠EDF

m∠arc EF  =  2 ⋅ 27°

m∠arc EF  =  54°

Problem 5 : 

If m∠KJL = (3x + 2)° and m∠KLJ = (7x - 32)°, find m∠arc KL. 

Solution  : 

In the diagram shown above, the inscribed angle m∠JKL intercepts the diameter JL. 

Then, 

m∠JKL  =  90°

In Δ PQR, 

m∠J + m∠K + m∠L  =  180°

Substitute. 

(3x + 2)° + 90° + (7x - 32)°  =  180°

3x + 2 + 90 + 7x - 32  =  180

10x + 60  =  180

Subtract 60 from each side. 

10x  =  120

Divide each side by 10.

x  =  12

Finding m∠KJL : 

m∠KJL  =  (3x + 2)°

Substitute x = 12

m∠KJL  =  [3(12) + 2]°

m∠KJL  =  [36 + 2]°

m∠KJL  =  38°

By Inscribed Angle Theorem, 

m∠arc KL  =  2 ⋅ m∠KJL

m∠arc KL  =  2 ⋅ 38°

m∠arc KL  =  76°

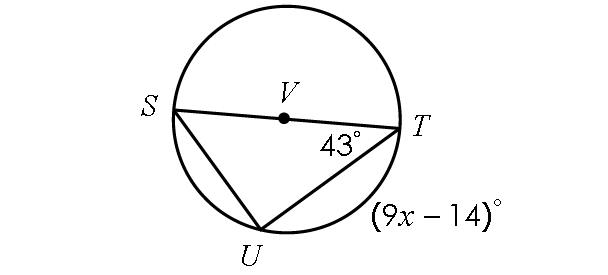
Problem 6 : 

Solve for x.

Solution  : 

In the diagram shown above, the inscribed angle m∠SUT intercepts the diameter ST. 

Then, 

m∠SUT  =  90°

In Δ SUT, 

m∠S + m∠U + m∠T  =  180°

Substitute. 

m∠S + 90° + 43°   =  180°

m∠S + 133°  =  180°

Subtract 133° from each side. 

m∠S  =  47°

m∠UST  =  47°

By Inscribed Angle Theorem, 

m∠arc UT  =  2 ⋅ m∠UST

Substitute. 

(9x - 14)°  =  2 ⋅ 47°

(9x - 14)°  =  94°

9x - 14  =  94

Add 14 to each side. 

9x  =  108

Divide each side by 9.

x  =  12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.