EXAMPLES OF INTEGRATION BY PARTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Integration by parts is one of the method basically used o find the integral when the integrand is a product of two different kind of function.
Formula :
∫u dv = uv-∫v du
|
Given Integral ∫log x dx ∫tan⁻ ¹ x dx ∫xⁿ log x dx ∫xⁿ tan⁻ ¹ x dx ∫xⁿ eax dx ∫xⁿ sin x dx ∫xⁿ cos x dx |
u log x tan⁻ ¹ x log x tan⁻ ¹ x xⁿ xⁿ xⁿ |
dv dx dx xⁿ dx xⁿ dx eax dx sin x dx cos x dx |
Example 1 :
Evaluate :
∫xexdx
Solution :
u = x, du = dx
dv = ex dx and v = ex
∫udv = uv-∫vdu
= xex-∫exdx
= xex-ex+C
∫ xex dx = ex(x-1)+C
Example 2 :
Evaluate :
∫xsinxdx
Solution :
u = x, du = dx
dv = sinx dx and v = -cosx
∫udv = uv-∫vdu
= x(-cosx)-∫(-cosx)dx
= -xcosx+∫cosxdx
∫ x sin x dx = -xcosx + sinx + C
Example 3 :
Evaluate :
∫xlogxdx
Solution :
u = logx, du = (1/x) dx
dv = dx and v = x2/2
∫udv = uv-∫vdu
= log x(x2/2) - ∫(x2/2)⋅(1/x)dx
= log x(x2/2) - (1/2)∫xdx
= log x(x2/2) - (1/2)(x2/2) + C
∫ x log x dx = (x2/2)log x - (x2/4) + C
Example 4 :
Evaluate :
∫xsec2xdx
Solution :
u = x, du = dx
dv = sec2x and v = tan x
∫udv = uv-∫vdu
= x(tan x) - ∫tan x dx
∫ xsec2x dx= x tanx - ln(secx) + C
Example 5 :
Evaluate :
∫xtan-1xdx
Solution :
u = x, du = (x2/2)dx
dv = tan-1 x dx and v = 1/(1+x2)
∫udv = uv-∫vdu
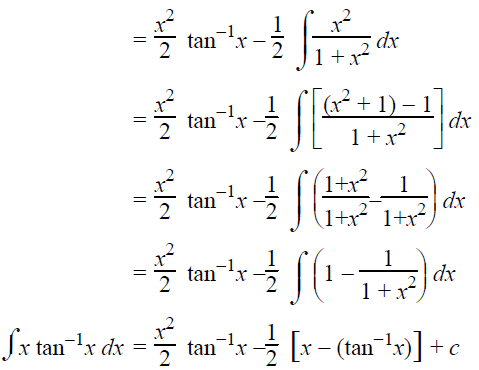
Example 6 :
Evaluate :
∫logxdx
Solution :
u = logx , du = 1/x
dv = dx and v = x
∫udv = uv-∫vdu
= logx(x) - ∫xdx
∫ log x dx = xlogx - (x2/2) + C
Example 7 :
Evaluate :
∫sin-1xdx
Solution :
u = sin-1x , du = 1/√(1-x2) dx
dv = dx and v = x
∫udv = uv-∫vdu
= xsin-1x-∫x (1/√(1-x2)) dx
= xsin-1x-∫ (x/√(1-x2)) dx
Here we may use substitution method to find integration.
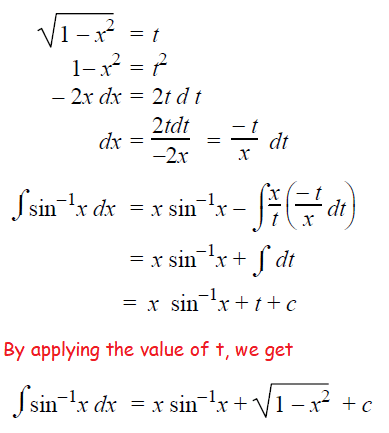
Example 8 :
Evaluate :
∫xsin2xdx
Solution :
sin2x = (1-cos2x)/2
∫x sin2x dx = ∫x (1-cos2x)/2 dx
= (1/2)[∫x(1-cos2x) dx]
= (1/2)[∫x dx - ∫x cos2x dx]
= (1/2)[(x2/2) - ∫x cos2x dx] ---(1)
Integrating x cos2x :
u = x and du = dx
dv = cos 2x and v = sin2x/2
∫udv = uv-∫vdu
= x(sin2x/2)-∫(sin2x/2) dx
= (x/2)sin2x-(1/2)∫sin2x dx
∫x cos2x dx = (x/2)sin2x+(1/4)cos 2x
Applying the integrated answer in (1), we get
= (1/2)(x2/2) - 1/2[(x/2)sin2x+(1/4)cos 2x] + C
= (x2/4) - (x/4)sin2x-(1/8)cos 2x + C
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
