INTEGRATION USING PARTIAL FRACTIONS EXAMPLES

Example 1 :

Integrate the following function with respect to x :

1/(x - 1) (x + 2)²

Solution :

Decompose the given rational function into partial fractions. 

1/(x - 1) (x + 2)²  =  A/(x - 1) + B/(x + 2) + C/(x + 2)²

1  =  A(x+2)² + B(x-1)(x+2) + C(x-1)

Plug x = 1

1  =  9A

A  =  1/9

Plug x = -2

1  =  C(-3)

C  =  -1/3

Plug x = 0

1  =  4A-2B-C

1  =  4(1/9) - 2B - (-1/3)

1  =  (4/9)- 2B + (1/3)

1 - (4/9) - (1/3)  =  -2B

-2B  =  (9 - 4 - 3)/9

-2B  =  2/9

B  =  -1/9

Integrate.

∫[1/(x - 1) (x + 2)²] dx

=  (1/9)∫(1/(x-1))dx-(1/9)∫(1/(x+2)-(1/3)∫(1/(x+2)² dx

=  (1/9)log(x-1) - (1/9)log (x+2)-(1/3)(1/(x+2)) + c

=  (1/9) [log(x - 1) - log(x + 2)] - (1/3)(1/(x+2)) + c

=  (1/9) [log(x - 1)/(x - 2)] - (1/3(x + 2)) + c

Example 2 :

Integrate the following function with respect to x :

(3x - 9)/(x - 1)(x + 2)(x² + 1)

Solution :

Decompose the given rational function into partial fractions. 

(3x - 9)/(x - 1)(x + 2)(x² + 1) 

  =  A/(x - 1) + B/(x + 2) + (Cx + D)/(x² + 1)

3x - 9  =  A(x+2)(x²+1)+B(x-1)(x²+1)+(Cx+D)(x-1)(x+2)

Plug x = 1

3 - 9  =  A(6)

-6  =  6A  ==>  A  =  -1

Plug x = -2

-6 - 9  =  B(-3)(5)

-15  =  -15B  ==>  B  =  1

Plug x = 0

- 9  =  2A - B - 2D

-9  =  2(-1) - 1 - 2D

-9  + 3  =  -2D

-6  =  -2D

D  =  3

3x - 9  =  A(x+2)(x²+1)+B(x-1)(x²+1)+(Cx+D)(x-1)(x+2)

Plug x = -1

- 12  =  A(1)(2) + B(-2)(2) + (-C+D)(-2)

-12  =  2A - 4B + 2C - 2D

-12  =  2(-1) - 4(1) + 2C - 2(3)

-12  =  -2 - 4 - 6 + 2C

2C  =  -12 + 12

C  =  0

Integrate.

∫[(3x - 9)/(x - 1)(x + 2)(x² + 1)] dx

  =   -∫1/(x - 1) dx + ∫1/(x + 2) dx + ∫ 3/(x² + 1) dx

  =  - log (x - 1) + log (x + 2) + 3 tan^-1(x)

  =  log (x + 2)/(x - 1) + 3  tan^-1(x) + c

Example 3 :

Integrate the following function with respect to x :

x³/(x - 1)(x - 2)

Solution :

x³/(x - 1)(x - 2)  =  x³/(x² - 3x + 2)

In the given rational fraction, the highest exponent of x in numerator is greater than the highest exponent of x in denominator. 

So, we can use long division to decompose the given rational function. 

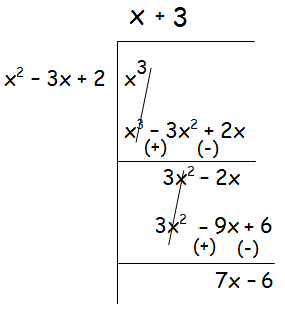
From the above long division, we have

x³/(x - 1)(x - 2)  =  (x + 3) + (7x - 6)/(x² - 3x + 2)

x³/(x - 1)(x - 2)  =  (x + 3) + (7x - 6)/(x - 1)(x - 2) ----(1)

Decompose (7x - 6)/(x - 1)(x - 2) into partial fractions. 

(7x - 6)/(x - 1)(x - 2)  =  A/(x - 1) + B(x - 2)

Simplify.

7x - 6  =  A(x - 2) + B(x - 1)

Plug x = 1

7(1) - 6  =  A(1 -2 ) + B(1 - 1)

1  =  A(-1)

A  =  -1

Plug x = 2

7(2) - 6  =  A(2 -2 ) + B(2 - 1)

8  =  B(1)

B  =  8

Therefore we have

(1)-----> x³/(x - 1)(x - 2)  =  (x + 3) - 1/(x - 1) + 8/(x - 2)

Integrate. 

∫[x³/(x - 1)(x - 2)] dx

  =  ∫(x + 3) dx -∫1/(x - 1) dx + 8∫1/(x - 2) dx

=  x²/2 + 3x -  log(x - 1) + 8log(x -  2) + C

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.