INTEGRATION AS LIMIT OF SUM EXAMPLES

Divide the interval [a,b] into n equal subintervals

[x₀, x₁], [x₁, x₂].................,[x_n-2, x_n-1], [x_n-1, x_n]

such that a = x₀ < x₁ < x₂ < .............< x_n-1< x_n < b.

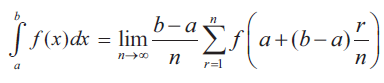
Evaluate the following integrals as the limits of sums:

Problem 1 :

Integral 0 to 1 (5x+4) dx

Solution :

f(x) = (5x+4), a = 0 and b = 1

f(a+(b-a)(r/n)) = f(0+(1-0)(r/n))

= f(r/n)

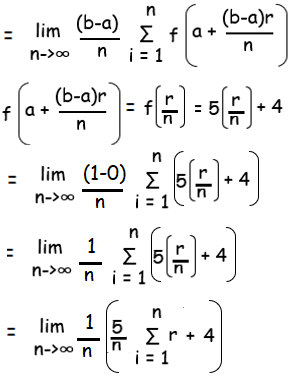
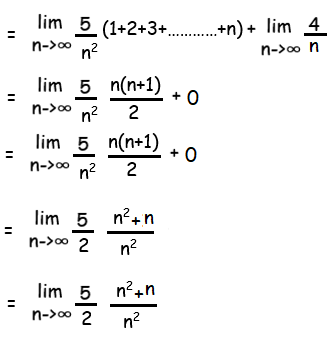
By applying the limit 

= (5/2) lim _n->∞ (1+1/n)

= (5/2)(1+0)

= 5/2

Problem 2 :

Integral 1 to 2 (4x²-1) dx

Solution :

f(x) = (5x+4), a = 1 and b = 2

f(a+(b-a)(r/n)) = f(1+(2-1)(r/n))

= f(1+r/n)

f(1+(r/n)) = (4(1+(r/n))²-1) 

 = 4(1+r²/n+2r/n) - 1

= 3+4r²/n+8r/n

By applying the limits,

= 3+(2/3)(2) + 4

= 3+4/3 + 4

= 7+(4/3)

= (21+4)/3

= 25/3

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.