INTEGRATE QUADRATIC FUNCTION IN THE DENOMINATOR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We have to express ax2+bx+c as sum or difference of two square terms to get the integrand in one of the standard forms.
Example 1 :
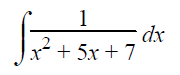
Solution :
We should represent the quadratic equation which is in the denominator in the form of sum or difference of squares.
Using completing the square method, we get
= x2 + 2 ⋅x ⋅ (5/2) + (5/2)2 - (5/2)2+7
= (x+(5/2))2+7-25/4
= (x+(5/2))2+3/4
= (x+(5/2))2+(√3/2)2
This exactly matches the formula,
∫1/(x2+a2) dx = 1/a tan-1(x/a) + c
Here a = √3/2 and x = x+(5/2)
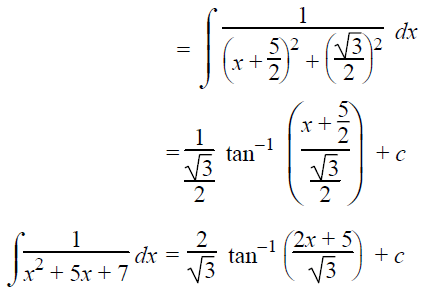
Example 2 :
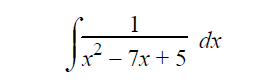
Solution :
Using completing the square method, we get
= x2 - 2 ⋅x ⋅ (7/2) + (7/2)2 - (7/2)2+5
= x2 - 2 ⋅x ⋅ (7/2) + (7/2)2 - (49/4)+5
= (x-(7/2))2+5-49/4
= (x-(7/2))2-29/4
= (x-(7/2))2-(√29/2)2
This exactly matches the formula,
∫1/(x2-a2) dx = (1/2a) [log (x-a)/(x+a)] + c
Here a = √29/2 and x = x-(7/2)
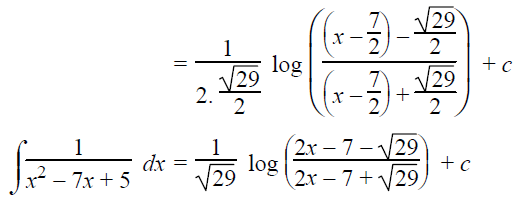
Integrating Quadratic Function in the Denominator with Square Root
Example 3 :
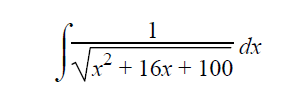
Solution :
Using completing the square method, we get
= x2 + 2⋅x⋅8 + 82-82+100
= (x+8)2 -64+100
= (x+8)2+36
= (x+8)2+62
This exactly matches the formula,
∫1/√(a2+x2) dx = log[x+√(a2+x2)] + c
Here a = 6 and x = x+8
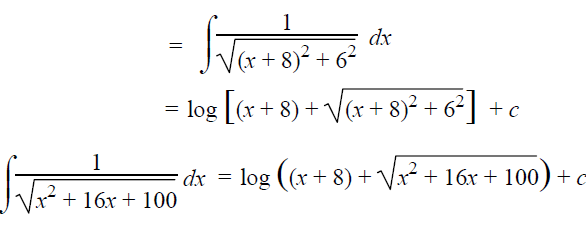
Example 4 :
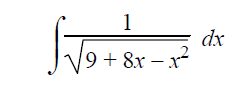
Solution :
Using completing the square method, we get
9+8x-x2 = -(x2-8x-9)
= -(x2 - 2⋅x⋅4 + 42-42-9)
= -[(x-4)2-16-9]
= -[(x-4)2-25]
= 52-(x-4)2
This exactly matches the formula,
∫1/√(a2-a2) dx = sin-1(x/a) + C
Here a = 5 and x = x-4
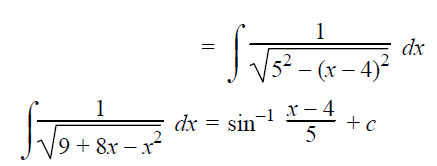
Integration of Rational Functions by Partial Fractions
Example 5 :
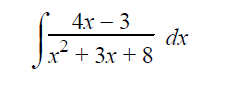
Using partial fraction, we are decomposing
∫(4x-3)/(x2+3x+8) dx
Numerator = A (Derivative of denominator) + B --(1)
4x-3 = A d(x2+3x+8)/dx + B
4x-3 = A (2x+3) + B
Equating the coefficients of x, we get
4 = 2A
A = 2
Equating constants, we get
-3 = 3A + B
By applying the value of A, we get
-3 = 6 + B
B = -9
Numerator = A (Derivative of denominator) + B
Dividing (1) by (x2+3x+8), we get
∫(4x-3)/(x2+3x+8) dx
= ∫2 (2x+3)/(x2+3x+8) dx - ∫9/(x2+3x+8) dx
= 2∫[(2x+3)/(x2+3x+8)]dx - 9∫[1/(x2+3x+8)] dx
By integrating 2∫[(2x+3)/(x2+3x+8)]dx :
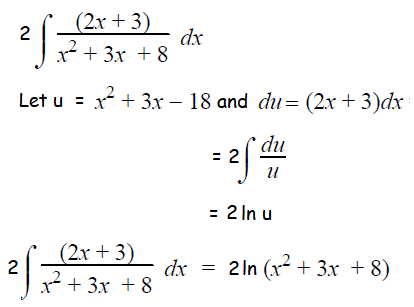
By integrating 9∫1/(x2+3x+8)dx :
Using completing the square method, we get
= x2 + 2⋅x⋅(3/2) + (3/2)2-(3/2)2+8
= (x+(3/2))2 + 8 - 9/4
= (x+(3/2))2 + 23/4
= (x+(3/2))2 + √(23/2)2
The second part exactly matches with the formula
∫1/(x2+a2) dx = 1/a tan-1(x/a) + c
Here x = x+(3/2) and a = √(23/2)
Using the above formula, we get
= 1/√(23/2) tan-1 (2x+3)/√23
= (2/√23) tan-1 (2x+3)/√23
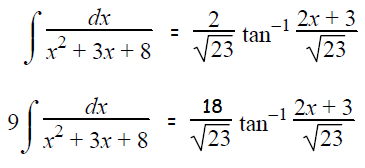
By combing the above results, we get
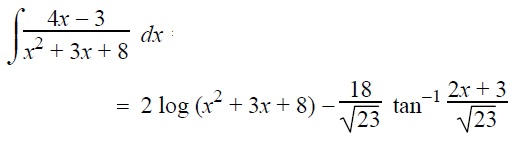
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 23)
Feb 27, 26 04:01 AM
Digital SAT Math Problems and Solutions (Part - 23) -
Digital SAT Math Problems and Solutions (Part - 22)
Feb 26, 26 08:43 PM
Digital SAT Math Problems and Solutions (Part - 22) -
10 Tricky SAT Math Questions with Answers
Feb 25, 26 08:07 AM
10 Tricky SAT Math Questions with Answers