INTEGERS ON NUMBER LINES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In basic mathematics, a number line is a picture of a graduated straight line that serves as abstraction for real numbers, denoted by . Every point of a number line is assumed to correspond to a real number, and every real number to a point.
Draw a line and mark some points at equal distance on it as shown in the figure.
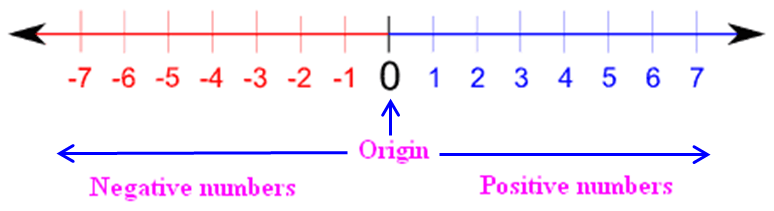
Mark a point as zero on it. Points to the right of zero are positive integers and are marked +1, +2, +3, etc. or simply 1, 2, 3 etc.
Points to the left of zero are negative integers and are marked –1, –2, –3 etc. In order to mark –6 on this line, we move 6 points to the left of zero.
Example 1 :
Represent +5 on the number line.
Solution :
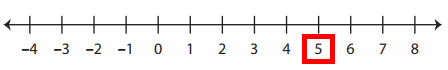
Example 2 :
Compare the numbers 3 and 6
Solution :
Let us locate the two numbers 3 and 6 on a number line and mark them.

Here, 6 comes to the right of 3.
Therefore "6" is greater than "3"
And 3 comes to the left of 6.
Therefore "3" is smaller than "6"
Example 3 :
Compare the numbers 6 and 9
Solution :
Let us locate the two whole numbers 6 and 9 on a number line and mark them.
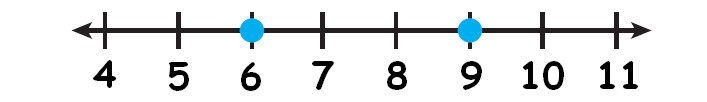
Here, 9 comes to the right of 6.
Therefore "9" is greater than "6"
And 6 comes to the left of 9.
Therefore "6" is smaller than "9"
Example 4 :
Order the numbers 12, 5, 9, 6, 1, 3 from least to greatest.
Solution :
Let us locate the numbers 12, 5, 9, 6, 1, 3 on a number line and mark them.

From the above number line, write the numbers from left to right to list them in order from least to greatest.
Thus, we get
1, 3, 5, 6, 9, 12
Example 5 :
In 2010, Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation ?
Solution :
Locate the two numbers 23 and 17 on a number line and mark them.
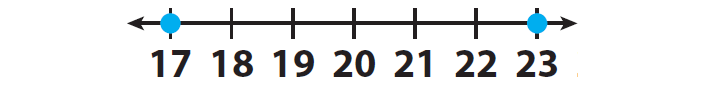
23 is to the right of 17 on the number line.
This means that 23 is greater than 17.
We can write the above situation in terms of inequality as 23 > 17.
17 is to the left of 23 on the number line.
This means that 17 is less than 23.
We can write the above situation in terms of inequality as 17 < 23.
There was more precipitation in 2010.
Example 6 :
Which expression can be used to find the change in the stock price for May and June?

a) −4 + 14 b) 4 − 14 c) −4 − 14 d) 14 − 4
Solution :
Price of stock in month of May --> Down 4, then -4
Price of stock in month of June --> Down 14, then -14
Price change from May to June = -4 - 14
So, option c is correct.
Example 7 :
The diving capsule is raised 150 meters. Write and evaluate an expression that represents the position of the capsule after it is raised
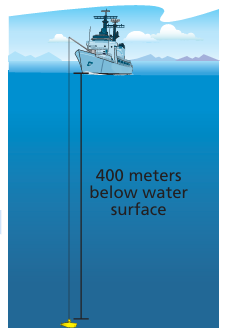
Solution :
The phrase below water surface indicates a negative integer. So, −400 represents the position of the capsule before it is raised.
Words The position of the capsule is raised 150 meters.
Expression −400 + 150
An expression is −400 + 150
The position of the capsule is −250 meters.
Example 8 :
The goal differential for a −3 soccer team is the difference between the number of goals scored by the team and the number of goals the team allows.
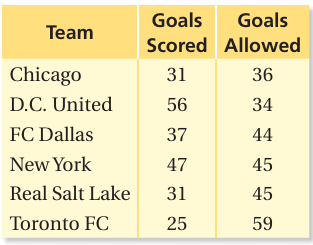
a. Use a number line to find the goal differential for each team.
b. Order the goal differentials from least to greatest. Which team has the lowest goal differential? Which team has the highest?
Solution :
a)
- Chicago ==> 31 - 36 ==> -5
- D.C. United ==> 56 - 34 ==> 22
- FC Dallas ==> 37 - 44 ==> -7
- New york ==> 47 - 45 ==> 2
- Real Salt Lake ==> 31 - 45 ==> -14
- Toronto FC ==> 25 - 59 ==> -34
b) Arranging from least to greatest,
-34, -14, -7, -5, 2, 22
Lowest goal = -34
Greatest goal = 22
D.C United has scored the highest goal.
Example 9 :
Describe the pattern 8, 5, 2, −1, −4, . . .. Then use a number line to find the next three numbers in the pattern.
Solution :
8, 5, 2, −1, −4, . . ..
8 - 5 ==> 3
5 - 2 ==> 3
Every term is decreased by 3,
- -4 - 3 ==> -7
- -7 - 3 ==> -10
- -10 - 3 ==> -13
The next three terms are -7, -10, -13.
Example 10 :
The temperature dropped 14°F in 5 hours. The final temperature is −8°F. What was the starting temperature? Explain how you found your answer.
Solution :
We can assume that the starting temperature was the temperature 5 hours ago. We know that the temperature now is the final temperature which is -8 degrees F. We are told that the temperature dropped 14 degrees over the last 5 hours. Therefore the starting temperature is...
-8 degrees + 14 degrees = 6 degrees F
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
