INTEGER INEQUALITIES WITH ABSOLUTE VALUES

The absolute value of a number is its distance from 0 on a number line. For example, the number "9" is 9 units away from zero. So its absolute value is 9.

Negative numbers are more interesting compared to positive numbers, because the number -4 is still 4 units away from 0. The absolute value of the number -4 is therefore positive 4.

The sign | | represents absolute value.

Now let us see some examples to know how to compare absolute values with integers.

Example 1 :

Evaluate the following :

|56 - 15| ⋅ 8 + |14|/2

Solution :

= |56 - 15| ⋅ 8 + |14|/2

= |41| ⋅ 8 + 14/2

= 41 ⋅ 8 + 7

  = 328 + 7

= 335

Example 2 :

Evaluate the following :

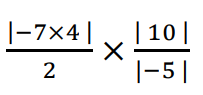
Solution :

= |-7 ⋅ 4|/2 ⋅ |10|/|-5|

= |-28|/2 ⋅ 10/5

= 28/2 ⋅ 2

= 14 ⋅ 2

= 28

Example 3 :

Compare the following :

Solution :

To compare the above numerical expressions, first we have to simplify both L.H.S and R.H.S separately.

L.H.S :

= |30|/|10| + |-2 + 7|/5 ⋅ 8

= 30/10 + 5/5 ⋅ 8

= 3 + 1 ⋅ 8

= 3 + 8

= 11

R.H.S :

= |-32|/8 - |9 ⋅ 2| + |4|

= -32/8 - |18| + |4|

= -4 - 18 + 4

= -18

By comparing answers on both sides L.H.S is greater than right hand side.

Hence,

|30|/|10| + |-2 + 7|/5 x 8 > |-32|/8 - |9 x 2| + |4|

Example 4 :

Compare the following :

Solution :

To compare the above numerical expressions, first we have to simplify both L.H.S and R.H.S separately.

L.H.S :

= |9 + 2| - |45|/|3|

= |11| - 45/3

= 11 - 15

= -4

R.H.S :

= |22 + 1| + |1|/|3| ⋅ 6

 = |23| + (1/3) ⋅ 6

 = 23 + (1 ⋅ 2)

 = 23 + 2

= 25

By comparing answers on both sides R.H.S is greater than L.H.S.

Hence, 

|9 + 2| - |45|/|3| < |22 + 1| + |1|/|3| x 6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.