INEQUALITIES IN TWO TRIANGLES WORKSHEET

1. If two sides of one triangle are congruent to two sides of another triangle, and the third side of the first is longer than the third side of the second, then prove that the included angle of the first triangle is larger than the included angle of the second triangle.

2. In triangles ABC and DEF, we have

AB ≅ DE

BC ≅ EF

AC = 12 inches

m∠B = 36°

m∠E = 80°

Which of the following is a possible length for DF ?

8 inches, 10 inches, 12 inches, 23 inches

3. In triangles RST and XYZ, we have

RT ≅ XZ

ST ≅ YZ

RS = 3.7 centimeters 

XY = 4.5 centimeters

m∠Z = 75°

Which of the following is a possible measure for m∠T ?

60°, 75°, 90°, 105°

4. You and a friend are flying separate planes. You leave the airport and fly 120 miles due west. You then change direction and fly W 30° N for 70 miles. (W 30° N indicates a north-west direction that is 30° north of due west.) Your friend leaves the airport and flies 120 miles due east. She then changes direction and flies E 40° S for 70 miles. Each of you has flown 190 miles, but which plane is farther from the airport ?

5. Find the following 

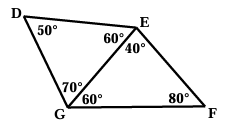
a) Find the shortest and longest segment in ∆DEG.

b) Find the shortest and longest segment in ∆EFG.

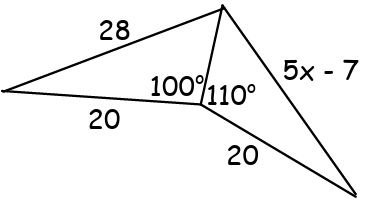
6. Write an inequality or pair of inequalities to describe the possible values of x

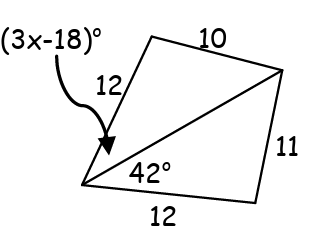
7. Write an inequality or pair of inequalities to describe the possible values of x

8. Starting from a point 10 miles north of Crow Valley, a crow flies northeast for 5 miles. Another crow, starting from a point 10 miles south of Crow Valley, flies due west for 5 miles. Which crow is farther from Crow Valley? Explain

1. Answer :

Let us consider two triangles ABC and DEF such that

AB  ≅  DE

BC ≅ EF

AC > DF

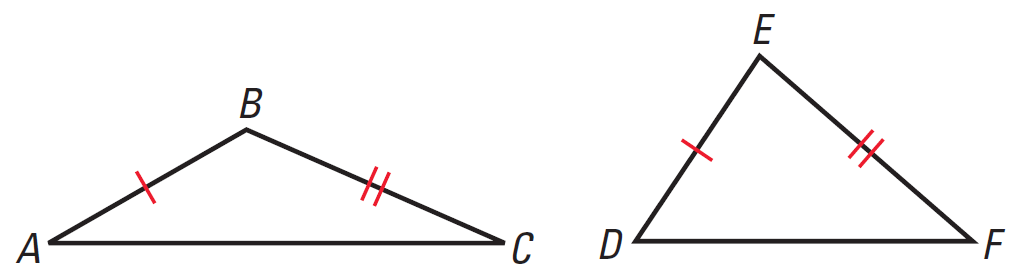
To Prove : m∠B > m∠E

Begin by assuming that m∠B  is not greater than m∠E. 

Then, it follows that either m∠B = m∠E or m∠B < m∠E. 

Case 1 : 

If m∠B = m∠E, then m∠B ≅ m∠E.

So, ΔABC ≅ ΔDEF by the SAS Congruence Postulate and AC = DF. 

Case 2 : 

If m∠B < m∠E, then AC < DF by the Hinge theorem.

Both conclusions contradict the given information that

AC > DF

So the original assumption that m∠B is not greater than m∠E cannot be correct. 

Therefore, 

m∠B > m∠E

2. Answer :  

From the given information, let us draw the two triangles ABC and DEF. 

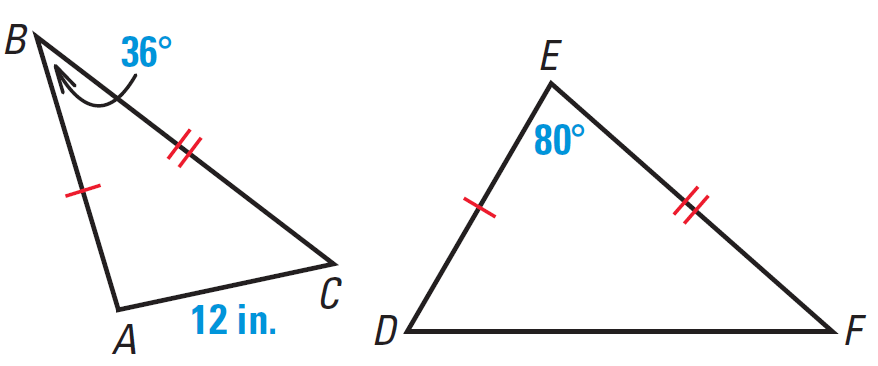
Because the included angle in triangle DEF is larger than the included angle in triangle ABC, the third side DF must be longer than AC.   

So, of the four choices, the only possible length for DF is 23 inches. The diagram of the two triangles ABC and DEF above shows that this is possible.  

3. Answer :

Because the third side in triangle RST is shorter than the third side in triangle XYZ, the included angle m∠T must be smaller than m∠Z. 

So, of the four choices, the only possible measure for m∠T is 60°. 

4. Answer : 

Begin by drawing a diagram, as shown below. Your flight is represented by triangle PQR and your friend's flight is represented by triangle PST.  

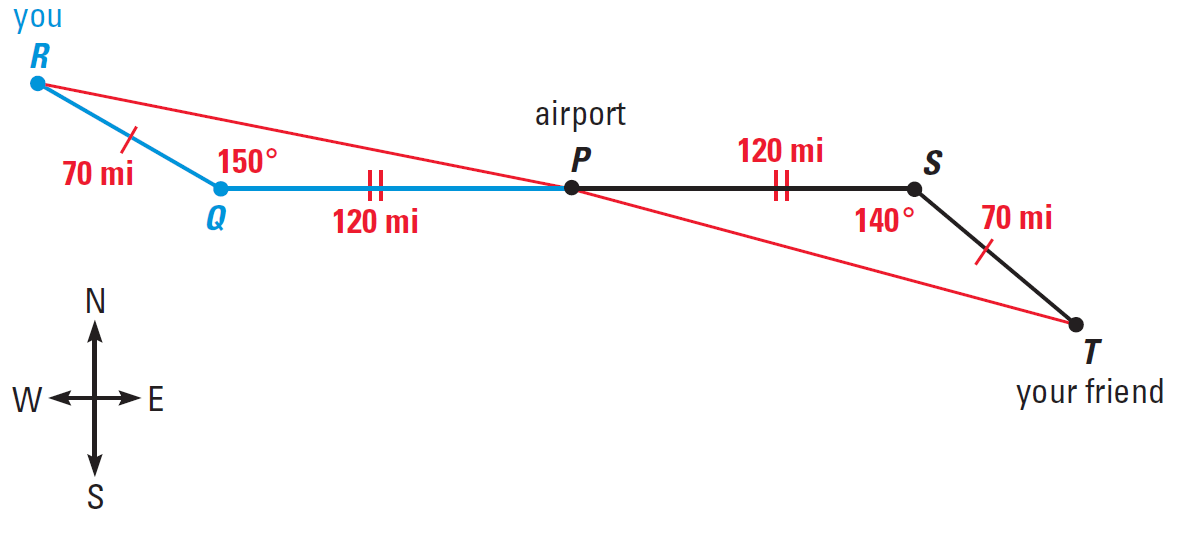
Because these two triangles have two sides that are congruent, you can apply the Hinge Theorem to conclude that RP is longer than TP.

So, your plane is farther from the airport than your friend’s plane.

5. Answer :

a) In triangle ∆DEG,

• the side which is opposite to the smaller side which is smaller side. 
• the side which is opposite to the longer side which is longer side.
• arranging the sides which is smaller to larger.

Opposite to 50° is GE

Opposite to 60° is DG

Opposite to 70° is DE

GE < DG < DE

b) In a triangle EGF,

The side which is opposite to 40° is GF

The side which is opposite to 60° is EF

The side which is opposite to 80° is GE

GF < EF < GE

6. Answer :

The side which is opposite to larger angle measure is larger.

5x - 7 > 28

Solving for x,

5x > 28 + 7

5x > 35

x > 35/5

x > 7

7. Answer :

By observing the given information,

11 > 10

The angle measures opposite to sides are 

42 > 3x - 18

42 + 18 > 3x

60 > 3x

60/3 > x

20 > x

8. Answer :

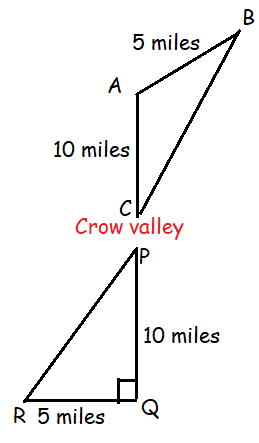
Considering the triangle ABC and PQR, unknown sides are PR and BC

Side opposite to <Q = 90 is PR

Side opposite to <A = obtuse angle

obtuse angle > right angle

BC > PR

Then the first crow is farther away comparing the another crow.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.