IDENTIFYING INTEGERS AND THEIR OPPOSITES

Understand that positive and negative numbers are used together to describe quantities having opposite directions or values.

Positive numbers are numbers greater than 0. Positive numbers can be written with or without a plus sign.

For example, 5 is the same as +5. Negative numbers are numbers less than 0.

Negative numbers must always be written with a negative sign.

For example, an integer which is 3 less than 0 is "-3". 

The above explained stuff has been illustrated in the picture given below.

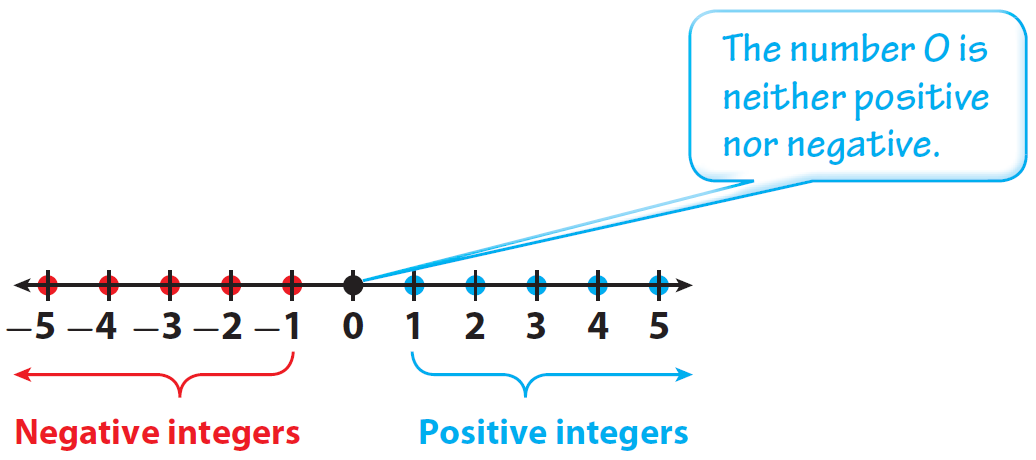
Identifying Integers and Their Opposites

To identify integers and their opposite signs, let us consider the following example. 

The elevation of a location describes its height above or below sea level, which has elevation 0. Elevations below sea level are represented by negative numbers, and elevations above sea level are represented by positive numbers.

The table shows the elevations of several locations in a state park.

Let us identify the integers on the number line given below to locate their elevations. 

Based on the information given above, we can have the following points in locating their elevations. 

1)   "0" is the point on the number line which represents sea level.

2)  Juniper Trail is closest to sea level. Because it is 3 ft below the sea level. 

3)  Little butte and Cradle creek are the two locations which are the same distance from sea level. Little butte is 5 ft above the sea level and Cradle creek is 5 ft below the sea level. 

Opposites

Two numbers are opposites if, on a number line, they are the same distance from 0 but on different sides of 0.

For example, 5 and -5 are opposites. 0 is its own opposite.

Integers are the set of all whole numbers and their opposites.

Real World Example

Positive and negative numbers can be used to represent real-world quantities.

For example, 3 can represent a temperature that is 3 °F above 0. -3 can represent a temperature that is 3 °F below 0.

Both 3 and -3 are 3 units from 0.

Integers and Opposites on a Number Line

Daniel kept track of the weekly low temperature in his town for several weeks. The table shows the low temperature in °F for each week.

Question 1 :

Graph the temperature from Week 3 and its opposite on a number line. What do the numbers represent ?

Step 1 :

The value from Week 3 is -4. 

Graph a point 4 units below 0.

Step 2 :

Graph the opposite of -4.

Graph a point 4 units above 0.

The opposite of -4 is 4.

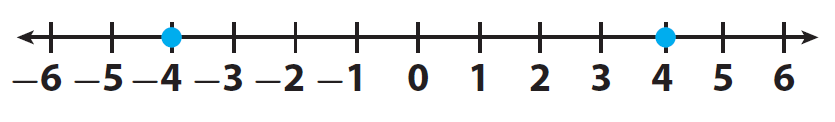
-4 represents a temperature that is 4 °F below 0 and 4 represents a temperature that is 4 °F above 0.

Question 2 :

The value for Week 5 is the opposite of the opposite of the value from Week 1. What was the low temperature in Week 5 ?

Step 1 :

Graph the value from Week 1 on the number line. 

The value from Week 1 is -1.

Step 2 :

Graph the opposite of -1.

The opposite of -1 is 1.

Step 3 :

Graph the opposite of 1.

The opposite of 1 is -1.

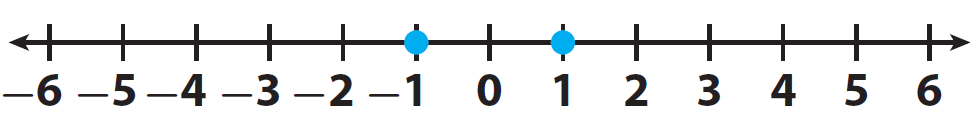
The opposite of the opposite of -1 is -1. The low temperature in Week 5 was -1 °F.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.