IDENTIFYING FUNCTIONS
A function is a special type of relation that pairs each domain value with exactly one range value.
In the following examples, give the domain and range of each relation. Tell whether the relation is a function. Explain.
Example 1 :

Solution :
Domain = {75, 68, 125}
Range = {2, 3}
(Even though 2 appears twice in the table, it is written only once when writing the range)
This relation is a function. Each domain value is paired with exactly one range value.
Example 2 :
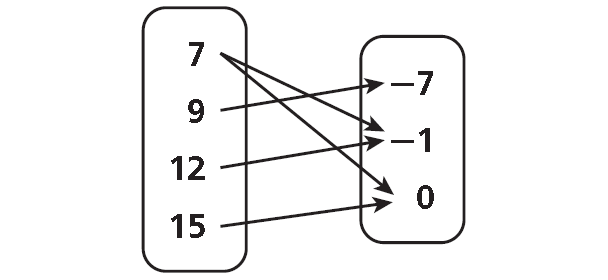
Domain = {7, 9, 12, 15}
Range = {-7, -1, 0}
Use the arrows to determine which domain values correspond to each range value.
This relation is not a function. Each domain value does not have exactly one range value. The domain value 7 is paired with the range values -1 and 0.
Example 3 :

Solution :
Draw lines to see the domain and range values.
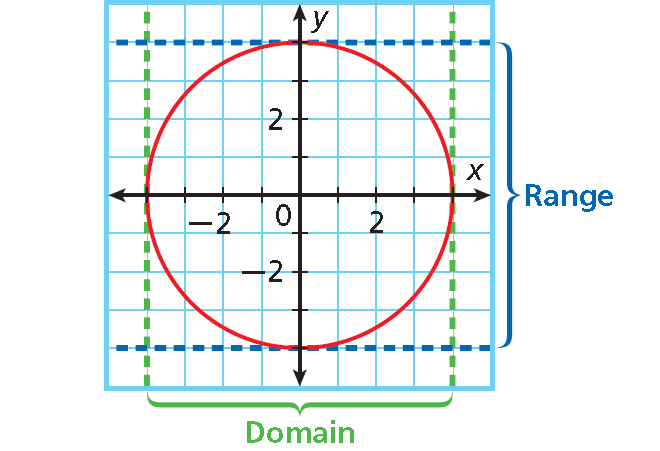
The domain is all x-values from -4 through 4, inclusive.
Domain : -4 ≤ x ≤ 4
The range is all y-values from -4 through 4, inclusive.
Range : -4 ≤ y ≤ 4
To compare domain and range values, make a table using points from the graph.

This relation is not a function because there are several domain values that have more than one range value. For example, the domain value 0 is paired with both 4 and -4.
Example 4 :
{(8, 2), (-4, 1), (-6, 2), (1, 9)}
Solution :
Domain = {8, -4, 6, 1}
Range = {2, 1, 9}
This relation is a function. Each domain value is paired with exactly one range value.
Example 5 :
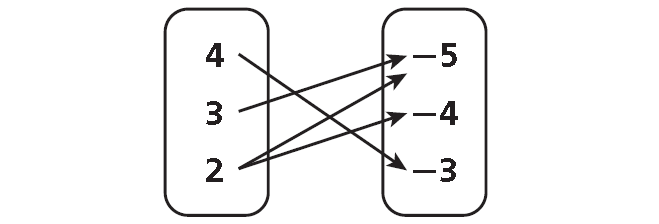
Solution :
Domain = {4, 3, 2}
Range = {-5, -4, -3}
This relation is not a function. Each domain value does not have exactly one range value. The domain value 2 is paired with the range values -5 and -4.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 12)
Sep 12, 25 09:50 PM
10 Hard SAT Math Questions (Part - 12) -
10 Hard SAT Math Questions (Part - 11)
Sep 11, 25 08:23 AM
10 Hard SAT Math Questions (Part - 11) -
Digital SAT Math Problems and Solutions (Part - 256)
Sep 10, 25 07:02 PM
Digital SAT Math Problems and Solutions (Part - 256)