IDENTIFYING FUNCTIONS WORKSHEET

In the following problems, give the domain and range of each relation. Tell whether the relation is a function. Explain.

Problem 1 :

Problem 2 :

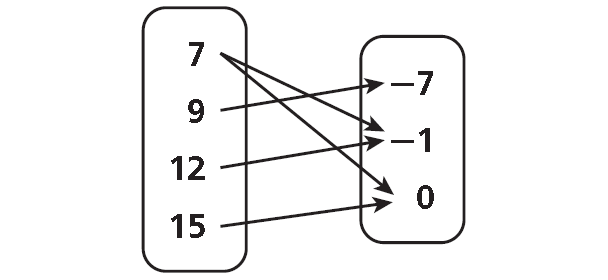
Problem 3 :

Problem 4 : 

{(8, 2), (-4, 1), (-6, 2), (1, 9)}

Problem 5 : 

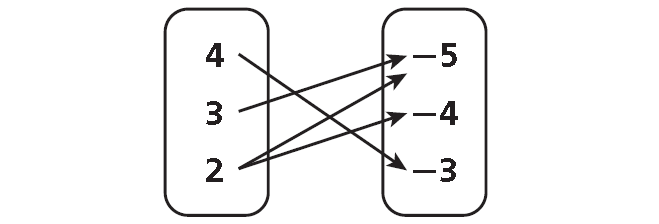
Problem 6 :

Let A = {-3, -2, -1, 1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. R is the relation which maps the elements from A to B using the rule f(x) = x². 

Problem 7 : 

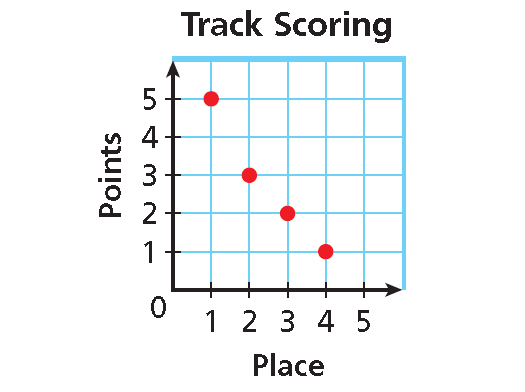
Problem 8 :

A = {1, 2, 3, 4} and B = {2, 5, 8, 11, 14} be two sets.

Let f : A--->B be a relation given by f(x) = 3x −1.

Answers

1. Answer :

Domain  =  {75, 68, 125}

Range  =  {2, 3}

(Even though 2 appears twice in the table, it is written only once when writing the range)

This relation is a function. Each domain value is paired with exactly one range value.

2. Answer :

Domain  =  {7, 9, 12, 15}

Range  =  {-7, -1, 0}

Use the arrows to determine which domain values correspond to each range value.

This relation is not a function. Each domain value does not have exactly one range value. The domain value 7 is paired with the range values -1 and 0.

3. Answer :

Draw lines to see the domain and range values.

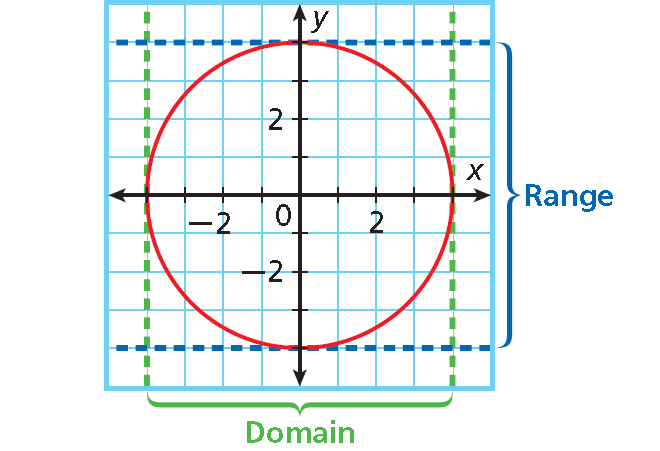
The domain is all x-values from -4 through 4, inclusive.

Domain : -4 ≤ x ≤ 4

The range is all y-values from -4 through 4, inclusive.

Range : -4 ≤ y ≤ 4

To compare domain and range values, make a table using points from the graph.

This relation is not a function because there are several domain values that have more than one range value. For example, the domain value 0 is paired with both 4 and -4.

4. Answer :

Domain  =  {8, -4, -6, 1}

Range  =  {2, 1, 9}

This relation is a function. Each domain value is paired with exactly one range value.

5. Answer :

Domain  =  {4, 3, 2}

Range  =  {-5, -4, -3}

This relation is not a function. Each domain value does not have exactly one range value. The domain value 2 is paired with the range values -5 and -4.

6. Answer :

R maps the elements from A to B using the rule

f(x)  =  x²

Then, we have

f(-3)  =  (-3)²  =  9

f(-2)  =  (-2)²  =  4

f(-1)  =  (-1)²  =  1

f(1)  =  1²  =  1

f(2)  =  2²  =  4

f(3)  =  3²  =  9

f(4)  =  4²  =  16

So, 

R  =  {(-3, 9), (-2, 4), (-1, 1), (1, 1), (2, 4), (3, 9), (4, 16)}

Therefore, 

Domain (R)  =  {-3, -2, -1, 1, 2, 3, 4}

Range (R)  =  {1, 4, 9, 16}

This relation is a function. Each domain value is paired with exactly one range value.

7. Answer :

To compare domain and range values, make a set of ordered pairs using points from the graph.

{(1, 5), (2, 3), (3, 2), (4, 1)}

Domain  =  {1, 2, 3, 4}

Range  =  {5, 3, 2, 2}

This relation is a function. Each domain value is paired with exactly one range value.

8. Answer :

A = {1, 2, 3, 4}; B = {2, 5, 8, 11, 14}; f (x) = 3x −1

Represent the relation f : A--->B by an arrow diagram. 

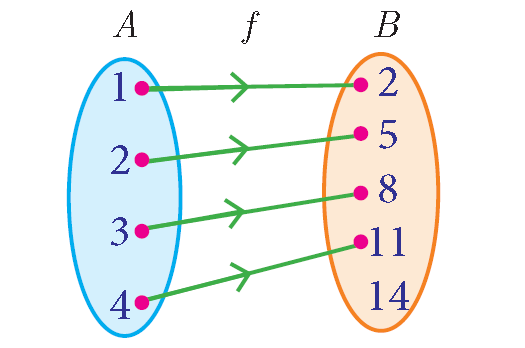
Domain  =  {1, 2, 3, 4}

Range  =  {2, 5, 8, 11}

This relation is a function. Each domain value is paired with exactly one range value.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.