IDENTIFYING FUNCTIONS FROM TABLES

About "Identifying functions from tables"

Identifying functions from tables :

A function assigns only output to each input. The value that is put into a function is the input. The result is the output.

Relationships between input values and output values can also be represented using tables. The values in the first column are the input values. The values in the second column are the output values. The relationship represents a function if each input value is paired with only one output value.

Identifying functions from tables - Examples

Example 1 :

Determine whether the relationship given in the table is a function.

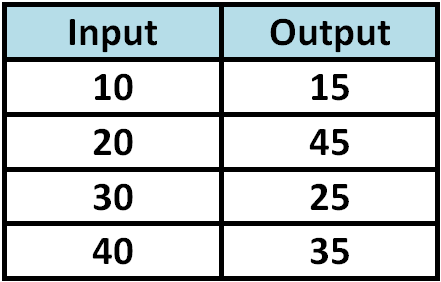
Solution :

Since each input value is paired with only one output value, the relationship given in the above table is a function.

Example 2 :

Determine whether the relationship given in the table is a function.

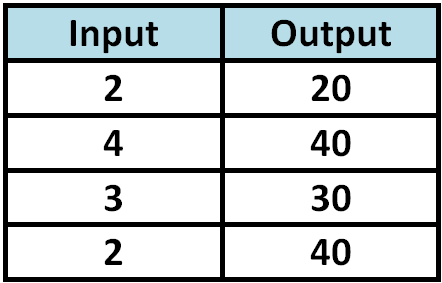
Solution :

Since 2 is paired with more than one output value (both 20 and 40), the relationship given in the above table is not a function.

Example 3 :

Determine whether the relationship given in the table is a function.

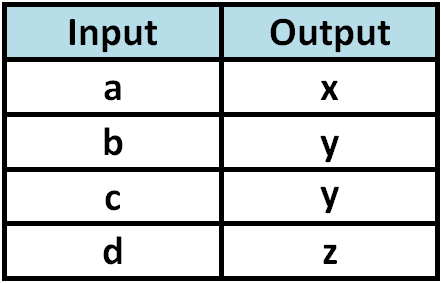
Solution :

Since each input value is paired with only one output value, the relationship given in the above table is a function.

Note :

In the above table, b and c have the same output value. However, b has only one output value y and c also has only one output value y. Moreover, no input value has more than one output value.

Example 4 :

Determine whether the relationship given in the table is a function.

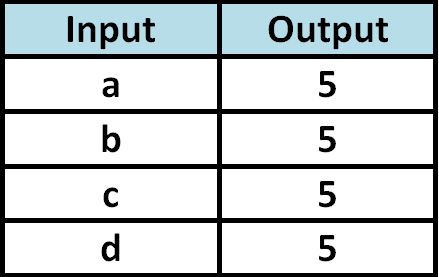
Solution :

Since each input value is paired with only one output value, the relationship given in the above table is a function.

Example 5 :

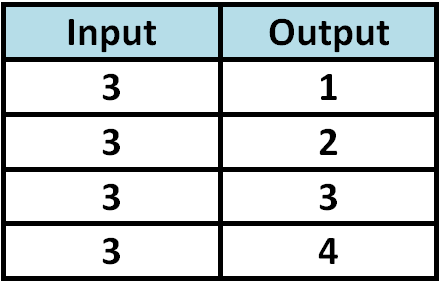
Determine whether the relationship given in the table is a function.

Solution :

Since the input value 3 is paired with more than one output value, the relationship given in the above table is not a function.

Example 6 :

Determine whether the relationship given in the table is a function.

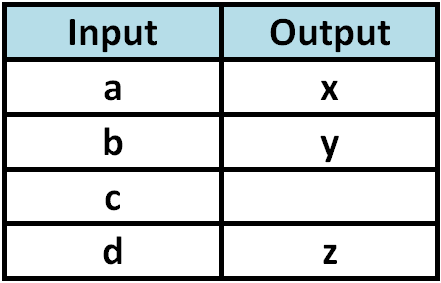
According to the rule of the function, there must be an output value for each input value. Since there is no output value for the input value "c", the relationship given in the above table is not a function.

Example 7 :

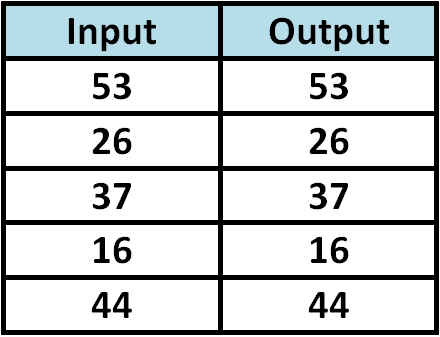
Determine whether the relationship given in the table is a function.

Solution :

Since each input value is paired with only one output value, the relationship given in the above table is a function.

Example 8 :

Is it possible for a function to have more than one input value but only one output value ? Provide an illustration to support your answer.

Solution :

Yes, a function can possibly have more than one input value, but only one output value.

Illustration :

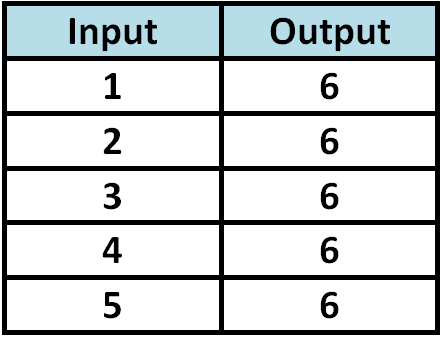
In the above table, there are five input values values (1, 2, 3, 4 and 5). But there is only one out put value 6.

According to the rule, each input value must have only one output value and no input value should have more than one output value.

In the above table, input value 1 has only one output value 6. The same has happened to the other input values 2, 3, 4 and 5 also. No input value has more than one out put value.

Hence, the relationship given in the above table is a function.