IDENTIFYING FUNCTIONS FROM GRAPHS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
For many functions we can obtain graphs. But, not every graph will represent a function. Following test will help us to determining, whether the given graph is a function or not.
Vertical Line Test
This is a tool which can be used to test whether the given graph represents a function or not.
The following are the steps of vertical line test :
Step 1 :
Draw a vertical line at any where on the given graph.
Step 2 :
We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.
Step 3 :
If the vertical line intersects the graph in at most one point, then the given graph represents a function.
If the vertical line intersects the graph in more than one point, then the given graph does not represent a function.
Caution :
For some graphs, the vertical line will intersect the graph in one point at one position and more than one point at a different position.
In the above situation, the graph will not represent a function.
Key Concept :
A graph represents a function only if every vertical line intersects the graph in at most one point.
Example 1 :
Use the vertical line test to determine whether the graph given below represents a function.
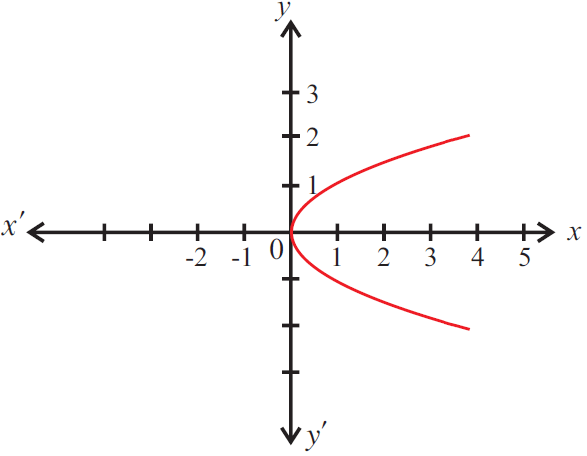
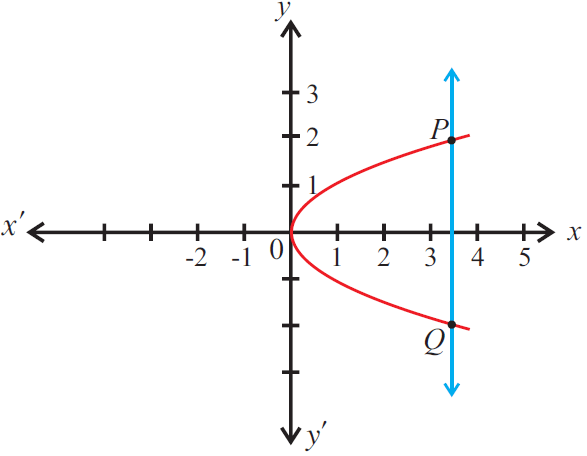
Solution :
The given graph does not represent a function as a vertical line cuts the graph at two points P and Q.
Example 2 :
Use the vertical line test to determine whether the graph given below represents a function.
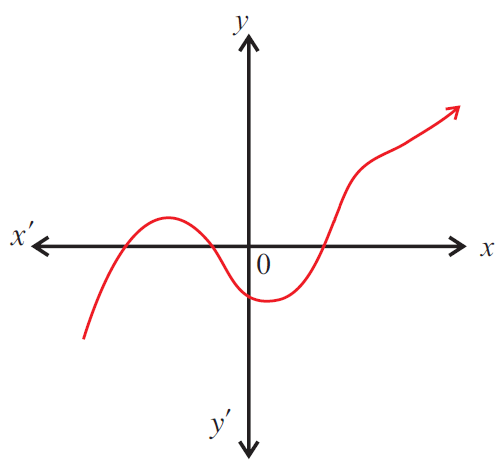
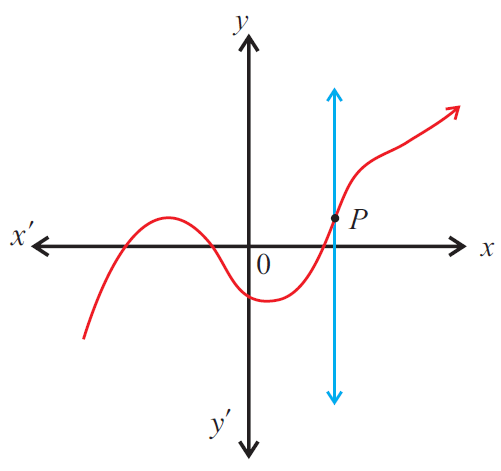
Solution :
The given graph represents a function as any vertical line will intersect the graph at most one point P.
Example 3 :
Use the vertical line test to determine whether the graph given below represents a function.
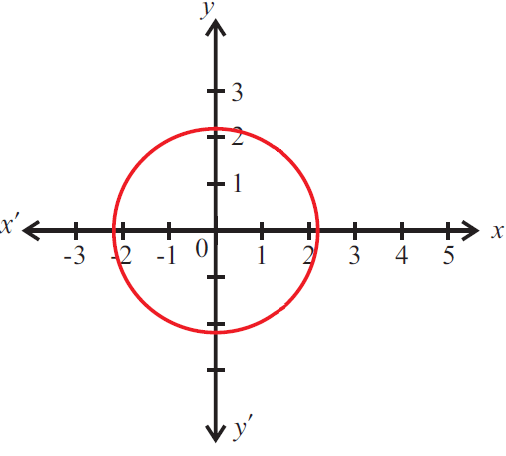
Solution :
The given graph does not represent a function as a vertical line cuts the graph at two points A and B.
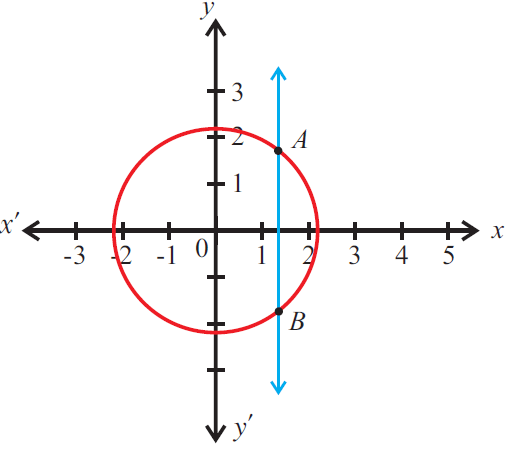
Example 4 :
Use the vertical line test to determine whether the graph given below represents a function.
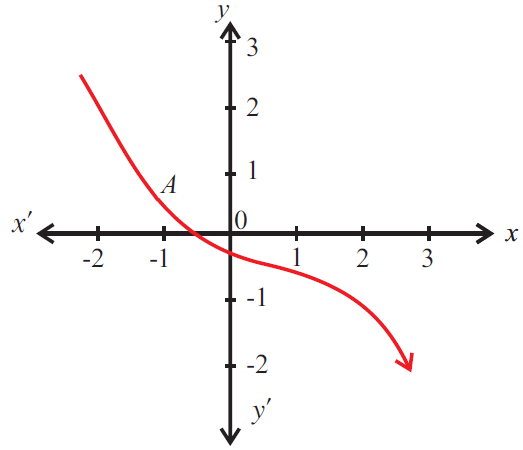
Solution :
The given graph represents a function as the graph satisfies the vertical line test.
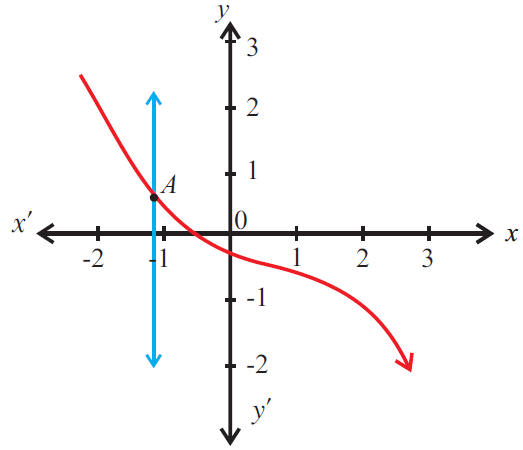
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

