IDENTIFYING EQUIVALENT EXPRESSIONS USING PROPERTIES

The properties of operations like commutative property of addition, commutative property of multiplication, distributive property etc. which we can use to identify equivalent expressions. 

Properties of Operations

1. Commutative Property of Addition : 

When adding, changing the order of the numbers does not change the sum.

Example : 

3 + 4  =  4 + 3

2. Commutative Property of Multiplication : 

When multiplying, changing the order of the numbers does not change the product.

Example : 

2 x 4  =  4 x 2

3. Associative Property of Addition : 

When adding more than twonumbers, the grouping of the numbers does not change the sum.

Example : 

(3 + 4) + 5  =  3 + (4 + 5)

4. Associative Property of Multiplication : 

When multiplying more than twonumbers, the grouping of the numbers does not change the product.

Example : 

(2 × 4) × 3  =  2 × (4 × 3)

5. Distributive Property : 

Multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.

Examples : 

6(2 + 4)  =  6(2) + 6(4)

8(5 - 3)  =  8(5) - 8(3)

6. Identity Property of Addition :

Adding zero to a number does not change its value.

Examples : 

9 + 0  =  0 + 9  =  9

7. Identity Property of Multiplication :

Multiplying a number by one does not change its value.

Examples : 

1 x 7  =  7 x 1  =  7

Solved Examples

Example 1 :

Use the properties of operations to determine if the expressions are equivalent.

3(x - 2) and 3x - 6

Solution :

Let us apply distributive property in the first expression 3(x - 2).

3(x - 2)  =  3(x) - 3(2)

3(x - 2)  =  3x - 6 ----- (1)

The second expression is

3x - 6 ----- (2)

From (1) and (2), the given two expressions are equivalent.

Example 2 :

Use the properties of operations to determine if the expressions are equivalent.

6x - 8 and 2(3x - 5)

Solution :

The first expression is

6x - 8 ----- (1)

Let us apply distributive property in the second expression 2(3x - 5).

2(3x - 5)  =  2(3x) - 2(5)

2(3x - 5)  =  6x - 10 ----- (2)

From (1) and (2), the given two expressions are not equivalent.

Example 3 :

Use the properties of operations to determine if the expressions are equivalent.

3x + (y + 2) and (3x + y) + 2

Solution :

The first expression is

3x + (y + 2) ----- (1)

Let us apply associative property of addition in the second expression. 

(3x + y) + 2  =  3x + (y + 2) ----- (2)

From (1) and (2), the given two expressions are equivalent.

Example 4 :

Use the properties of operations to determine if the expressions are equivalent.

2 - 2 + 5x and 5x

Solution :

Let us simplify the first expression 

2 - 2 + 5x  =  5x ----- (1)

The second expression is

5x ----- (2)

From (1) and (2), the given two expressions are equivalent.

Example 5 :

Use the properties of operations to determine if the expressions are equivalent.

2 + x and (1/2)(4 + x)

Solution :

The first expression is

2 + x ----- (1)

Let us apply distributive property in the second expression (1/2)(4 + x).

(1/2)(4 + x)  =  (1/2)(4) - (1/2)(x)

(1/2)(4 + x)  =  2 - x/2 ----- (2)

From (1) and (2), the given two expressions are not equivalent.

Example 6 :

Jamal bought 2 packs of stickers and 8 individual stickers. Use x to represent the number of stickers in a pack of stickers and write an  expression to represent the number of stickers Jamal bought. Is the expression equivalent to 2(4+x) ? Check your answer with algebra tile models.

Solution :

Given : There are x number of stickers in pack.

Then, the number of stickers in 2 packs is

2x

Jamal bought 2 packs of stickers and 8 individual stickers.

The expression which represents the above situation is

2x + 8

Let us apply distributive property in the expression 2x + 8.

2x + 8  =  2(x) + 2(4)

2x + 8  =  2(x + 4)

Let us apply commutative property of addition inside the parenthesis of 2(x + 4)

2(x + 4)  =  2(4 + x)

Yes, the expression which represents the number of stickers Jamal bought is equivalent to 2(4 + x).

Using algebra tiles :

2(4 + x) ----- (1)

Apply distributive property in the expression 2(4+x)

  2(4 + x)  =  2(4) + 2(x)

2(4 + x)  =  8 + 2x

Apply commutative property of addition in 8 +2x

2(4 + x)  =  2x + 8 ----- (2)

Now, let us use algebra tiles to model the two expressions 2(4 + x) and 2x + 8. 

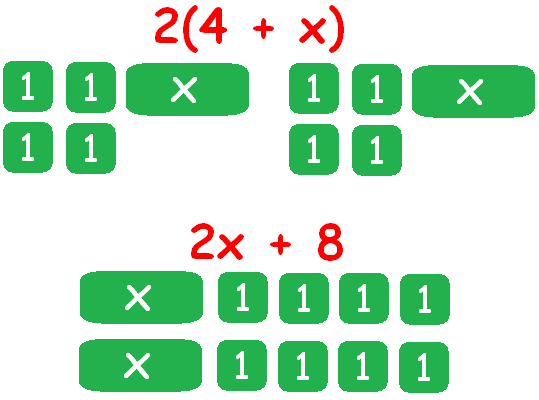
The expressions 2(4 + x) has two x tiles and eight 1 tiles. The expressions  2x + 8 also has two x tiles and eight 1 tiles. 

Hence, 2(4 + x) and 2x + 8 are equivalent.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.