IDENTIFYING AND REPRESENTING FUNCTIONS

Example 1 :

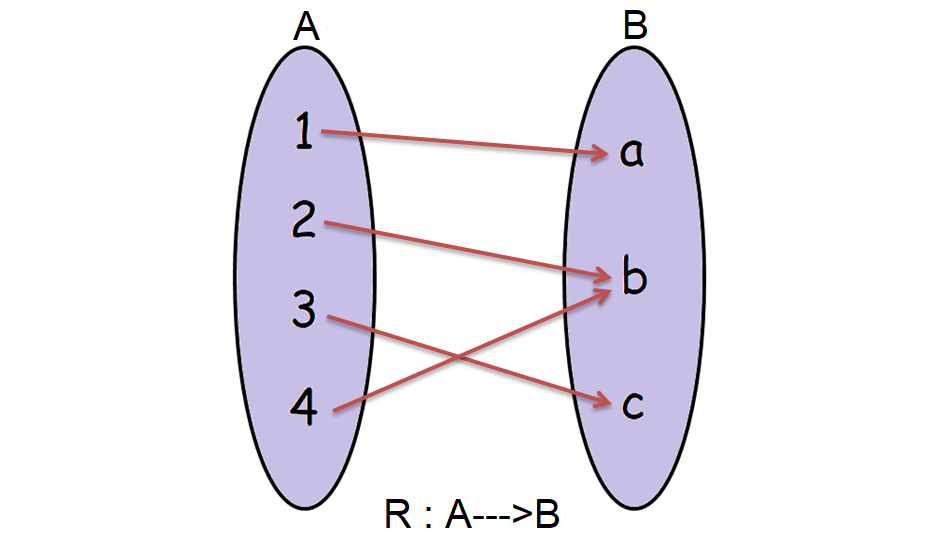
Let A  =  {1, 2, 3, 4} and B  =  {a, b, c}. 

Consider the relation R given below which maps the elements from A to B. 

R  =  {(1, a), (2, b), (3, c), (4, b)}

Determine whether the relationship R is a function.

Solution :

In the above relation R, 

Domain (R)  =  A

And also, every element of A has only one image in B. 

So, the relation R is a function. 

It has been illustrated in the picture shown below. 

Example 2 :

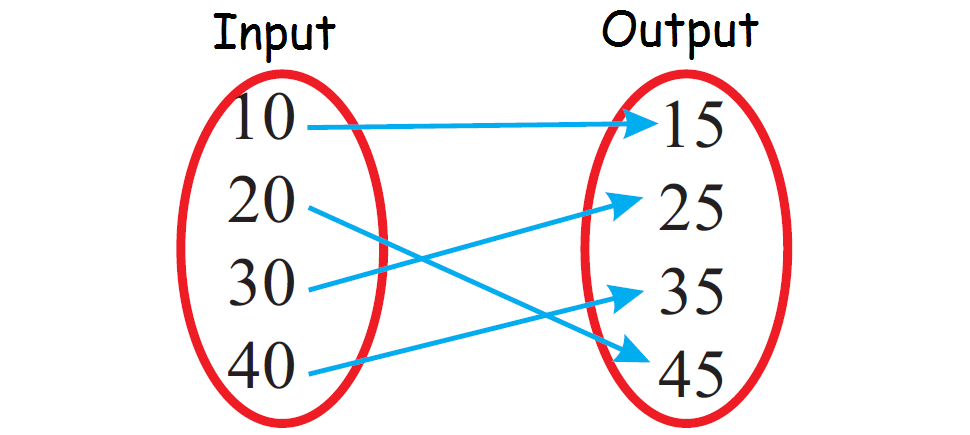
Determine whether the relationship given in the mapping diagram is a function.

Solution :

Since each input value is paired with only one output value, the relationship given in the above mapping diagram is a function.

Example 3 :

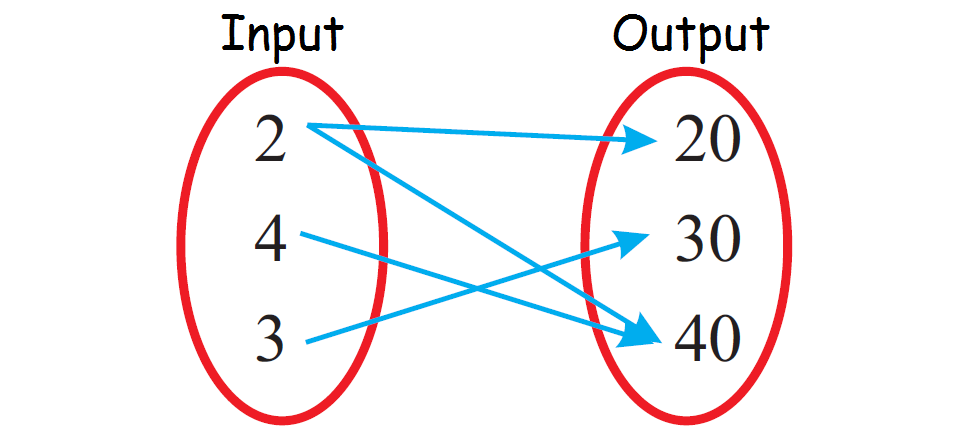
Determine whether the relationship given in the mapping diagram is a function.

Solution :

Since 2 is paired with more than one output value (both 20 and 40), the relationship given in the above mapping diagram is not a function.

Example 4 :

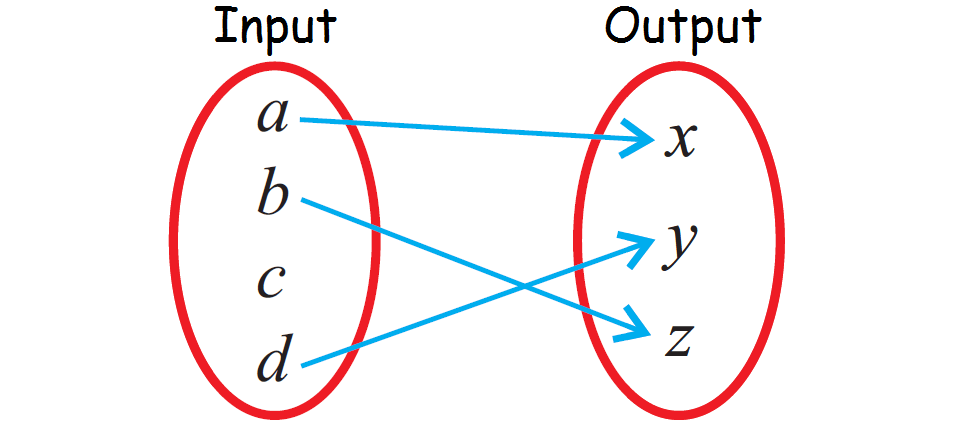
Determine whether the relationship given in the mapping diagram is a function.

Solution :

Since the input value "c" is not paired with any output value, the relationship given in the above mapping diagram is not a function.

Example 5 :

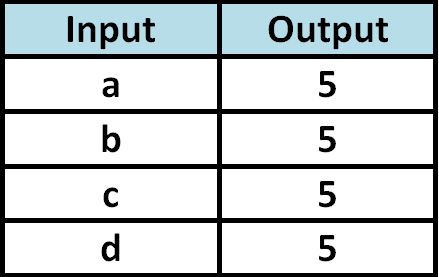
Determine whether the relationship given in the table is a function.

Solution :

Since each input value is paired with only one output value, the relationship given in the above table is a function.

Example 6 :

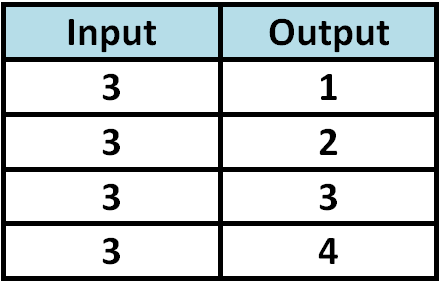
Determine whether the relationship given in the table is a function.

Solution :

Since the input value 3 is paired with more than one output value, the relationship given in the above table is not a function.

Example 7 :

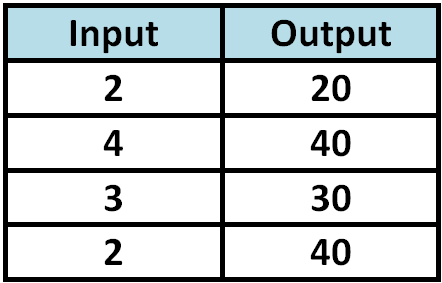
Determine whether the relationship given in the table is a function.

Solution :

Since 2 is paired with more than one output value (both 20 and 40), the relationship given in the above table is not a function.

Example 8 :

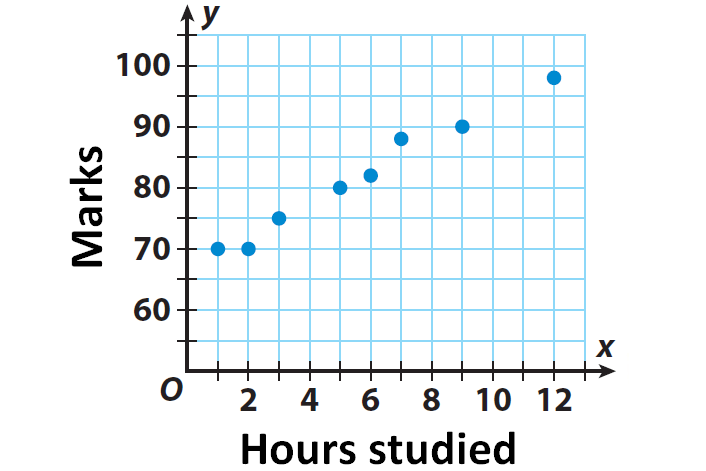
The graph given below shows the relationship between the number of hours students spent studying for an exam and the marks scored in the exam. Determine whether the relationship represented by the graph is a function. 

Solution :

From the graph, it is clear that if a student spends 2 hours for studying, he/she will be able to score 70 marks in the exam. And if he spends 9 hours for studying, he will be able to score 90 marks in the exam. 

So, we can consider the number of hours of studying as input values and marks scored in the exam as output values.

The points represent the following ordered pairs in the form (input, output) or (x, y) :

(1, 70), (2, 70), (2, 85), (3, 75), (5, 80), (6, 82), (7, 88), 

(9, 90), (9, 95) and (12, 98). 

In the above order pairs, there is only one output value for each input value. And no input value has more than one output value. 

Since, there is only one output value for each input value, the relationship represented by the graph is a function. 

Example 9 :

The graph shows the relationship between the heights and weights of the members of a basketball team. Is the relationship represented by the graph a function ? Explain.

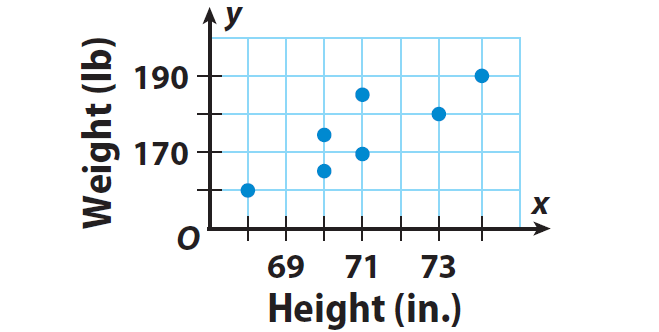
Solution :

From the graph, it is clear that if the height of a member is 73 inches, his weight will be 180 lbs. 

So, we can consider the height as input value and weight as output value.

The points represent the following ordered pairs in the form (input, output) or (x, y) :

(68, 160), (70, 165), (70, 175), (71, 170), (71, 185),

 (73, 180) and (74, 190). 

Notice that 70 is paired with both 165 and 175, and 71 is paired with both 170 and 185. These input values are paired with more than one output value.

Since, there is more than one output value for the input values 70 and 71, the relationship represented by the graph is not a function. 

Example 10 : 

Use the vertical line test to determine whether the following graph represents a function.

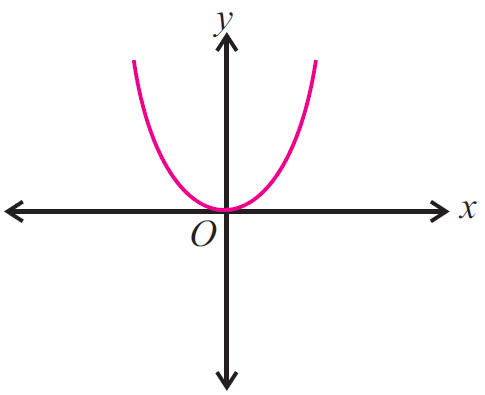
Solution :

Step 1 : 

Draw a vertical line at any where on the given graph. 

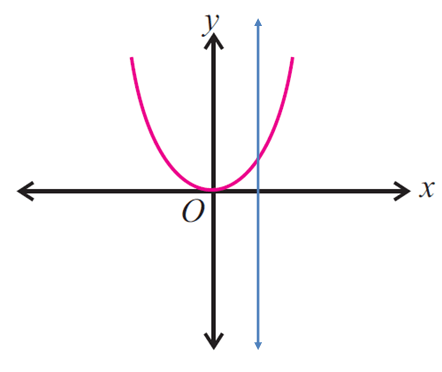
Step 2 : 

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 : 

In the above graph, the vertical line intersects the graph in at most one point, then the given graph represents a function. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.