IDENTIFYING A RIGHT TRIANGLE

We can use the converse of the Pythagorean Theorem to determine whether a triangle is a right triangle when the lengths of the three sides are given. 

Converse of the Pythagorean Theorem

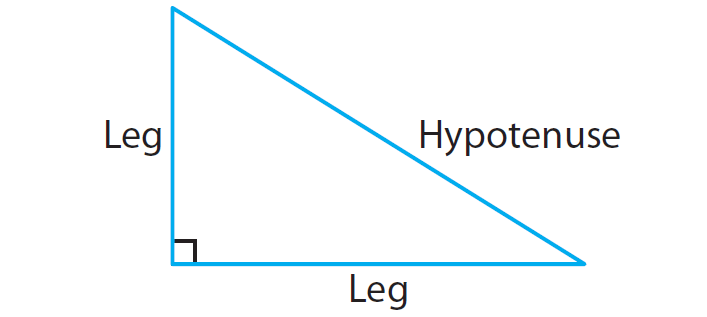
The Pythagorean Theorem states that if a triangle is a right triangle, then, the sum of the squares of the lengths of the  legs is equal to the square of the length of the hypotenuse.

That is, if a and b are legs and c is the hypotenuse, then

a² + b²  =  c²

The converse of the Pythagorean Theorem states that if a² + b²  =  c², then the triangle is a right triangle.

Example 1 :

Determine whether triangle with the side lengths given below is a right triangle.

9 inches, 40 inches, and 41 inches

Solution :

Step 1 :

Let a  =  9, b  =  40, and c  =  41.

(Always assume the longest side as "c")

Step 2 :

Find the value of a² + b². 

a² + b²  =  9² + 40²

a² + b²  =  81 + 1600

a² + b² -----(1)

Step 3 :

Find the value of c². 

c²  =  41²

c²  =  1681 -----(2)

Step 4 :

From (1) and (2), we get

a² + b²  =  c²

By the converse of Pythagorean theorem, the triangle with the side lengths 9 inches, 40 inches, and 41 inches is a right triangle. 

Example 2 :

Determine whether triangle with the side lengths given below is a right triangle.

8 meters, 10 meters, and 12 meters

Solution :

Step 1 :

Let a  =  8, b  =  10, and c  =  12.

(Always assume the longest side as "c")

Step 2 :

Find the value of a² + b². 

a² + b²  =  8² + 10²

a² + b²  =  64 + 100

a² + b²  =  164 -----(1)

Step 3 :

Find the value of c². 

c²  =  12²

c²  =  144 -----(2)

Step 4 :

From (1) and (2), we get

a² + b²  ≠  c²

By the converse of Pythagorean theorem, the triangle with the side lengths 8 meters, 10 meters, and 12 meters is not a right triangle. 

Example 3 :

Determine whether triangle with the side lengths given below is a right triangle.

14 cm, 23 cm, and 25 cm

Solution :

Step 1 :

Let a  =  14, b  =  23, and c  =  25.

(Always assume the longest side as "c")

Step 2 :

Find the value of a² + b². 

a² + b²  =  14² + 23²

a² + b²  =  196 + 529

a² + b²  =  725 -----(1)

Step 3 :

Find the value of c². 

c²  =  25²

c²  =  625 -----(2)

Step 4 :

From (1) and (2), we get

a² + b²  ≠  c²

By the converse of Pythagorean theorem, the triangle with the side lengths 14 cm, 23 cm, and 25 cm is not a right triangle. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.