IDENTIFY TRAPEZIUMS

What is trapezium ?

A quadrilateral in which one pair of opposite sides is parallel called trapezium.

Various types of trapeziums are,

• A right trapezoid
• An acute trapezoid
• obtuse trapezoid
• isosceles trapezoid
• parallelogram

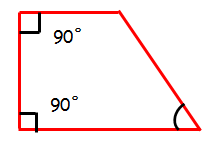
Right trapezoid :

A right trapezoid (also called right-angled trapezoid) has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.

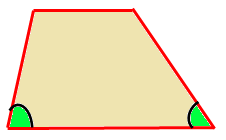
Acute Trapezoid :

An acute trapezoid has two adjacent acute angles on its longer base edge

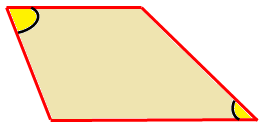
Obtuse Trapezoid :

An obtuse trapezoid has one acute and one obtuse angle on each base.

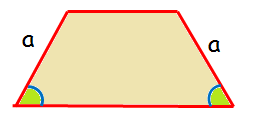
Isosceles Trapezoid :

An isosceles trapezoid is a trapezoid where the sides (legs) have the same length, and the base angles have the same measure. It has reflection symmetry. This is possible for acute or right trapezoids.

Parallelogram :

A parallelogram is a trapezoid with two pairs of parallel sides. A parallelogram has central 2-fold rotational symmetry (or point reflection symmetry). It is possible for obtuse or right trapezoids.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.