IDENTIFY THE DIRECTION A PARABOLA OPENS

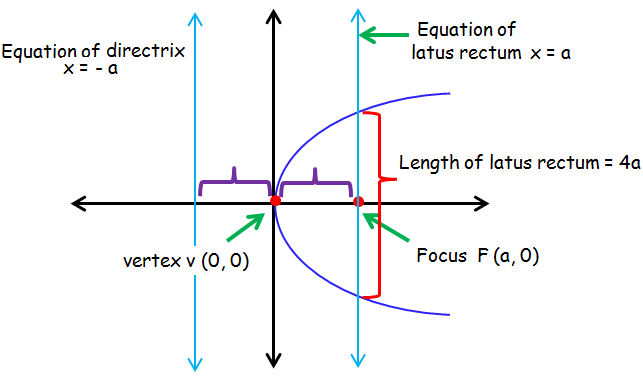
Parabola Symmetric About X-Axis and Opens to the Right

y² = 4ax is the standard equation of the parabola which is symmetric about x axis and open rightward.

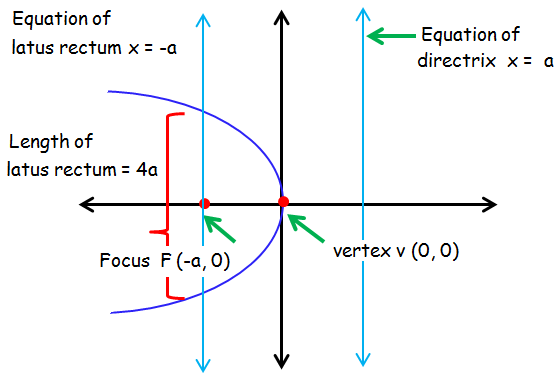
Parabola Symmetric About X-axis and Opens to the Left

y² = -4ax is the standard equation of the parabola which is symmetric about x axis and open rightward.

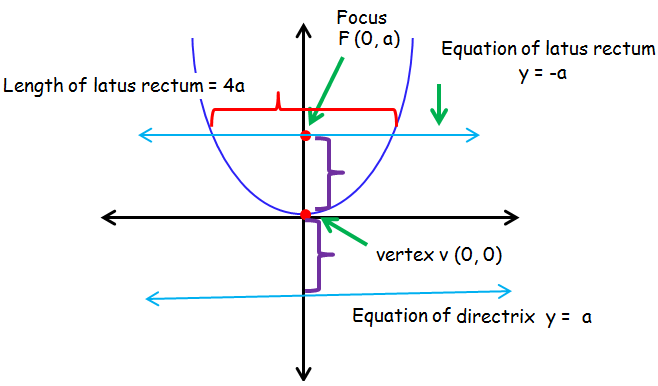
Parabola Symmetric About Y-Axis and Opens Up

x² = 4ay is the standard equation of the parabola which is symmetric about y axis and open upward.

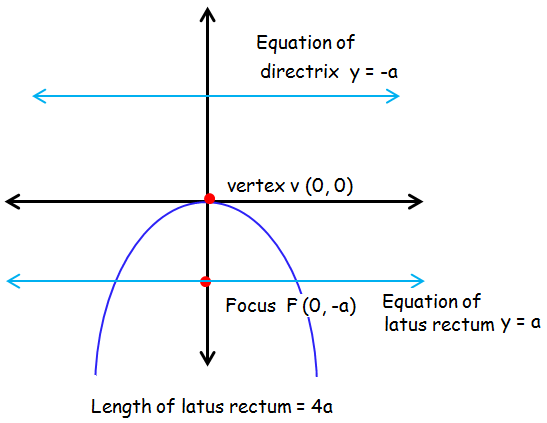
Parabola Symmetric About Y-Axis and Opens Down

x² = -4ay is the standard equation of the parabola which is symmetric about y axis and open downward.

Example 1 :

From the given equation of the parabola, find the direction it opens?

x² = -16y

Solution :

The given parabola is having square for the variable x, it is symmetric about y-axis.

To decide in which direction does it open, we have to look into the sign. It has negative sign in front of 16y, so the parabola opens downward.

Example 2 :

From the given equation of the parabola, find in which direction it opens?

y² - 8y - x + 19 = 0

Solution :

Convert the given equation of  parabola to standard form.

y² - 8y = x - 19

y² - 2y(4) + 4² - 4² = x - 19

(y - 4)² = x - 19 + 16

(y - 4)² = x - 3

Let Y = y - 4 and X = x  - 3.

Y² = X

Since the parabola is having square for the variable y, it is symmetric about X-axis.

Since X is positive, the parabola opens to the right.

Example 3 :

For the provided graph of a parabola, determine key features given below.

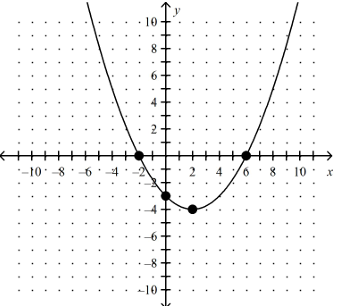
a) Direction of Opening

b) Number of Zeroes

c) Location of Zeroes

d) y-intercept

e) Axis of Symmetry

f) Max/Min Value

g) Vertex

Solution :

a) From the figure shown, the parabola opens up.

b) There are two zeroes.

c) Zeroes are -2 and 6.

d) y-intercept is -3

e) Axis of Symmetry is at x = 2

f) It has minimum value at -4.

g) Vertex is at (2, -4).

Equation of parabola :

y = a(x - h)² + k

y = a(x - 2)² + (-4)

y = a(x - 2)² - 4

Applying the point (6, 0), we get

0 = a(6 - 2)² - 4

4 = a(4)²

16a = 4

a = 4/16

a = 1/4

y = (1/4)(x - 2)² - 4

So, the required equation of the parabola is 

y = (1/4)(x - 2)² - 4

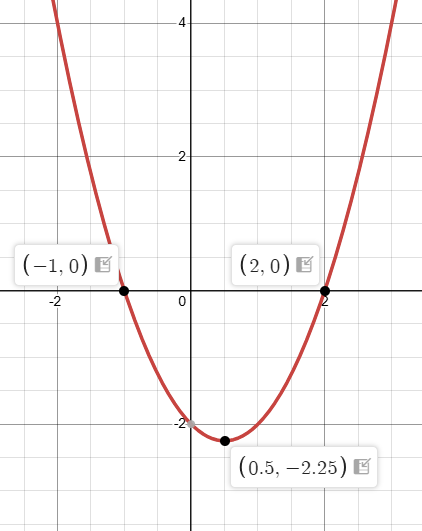
Example 4 :

For the parabola y = x² − x − 2, determine the vertex, the axis of symmetry, the intercepts, and draw the graph

Solution :

y = x² − x − 2

y = x² − (2/2)x − 2

y = x² − 2x(1/2) + (1/2)² - (1/2)² − 2

y = (x - 1/2)² − (1/4) − 2

y = (x - 1/2)² − (9/4)

The vertex of the parabola is (1/2, -9/4)

Axis of symmetry x = 1/2

Example 5 :

Write an equation of a parabola with vertex (−1, 4) and focus (−1, 2)

Solution :

Distance between vertex and focus

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(-1 + 1)² + (2 - 4)²

= √0² + (-2)²

= √4

a = 2

From the given vertex and focus, the parabola is symmetric about y-axis and opens downward.

(x - h)² = -4a(y - k)

(x - (-1))² = -4(2)(y - 4)

(x + 1)² = -8(y - 4)

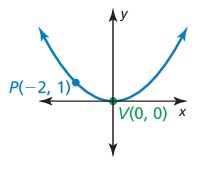
Example 6 :

The distance from point P to the directrix is 2 units. Write an equation of the parabola.

Solution :

Distance between vertex and focus = distance between vertex and directrix

a = 2

The parabola is symmetric about y-axis and opens upward.

(x - h)² = 4a(y - k)

The parabola passes through the point (-2, 1),

(x - (-2))² = 4(2)(y - 1)

(x + 2)² = 8(y - 1)

Example 7 :

Which of the following are possible coordinates of the point P in the graph shown? Explain

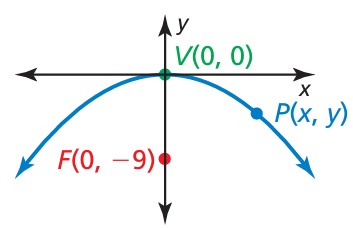
a)  (-6, -1)   b) (3, -1/4)   c) (4, -4/9)    d)  (1, 1/36)

e)  (6, -1)   f) (2, -1/18)

Solution :

From the given figure, the parabola is symmetric about y-axis and open downward.

(x - h)² = 4(2)(y - k)

a = 9

(x - 0)² = -4(9)(y - 0)

x² = -36y

Option a :

The point (-6, -1) will not be the point P, because in the shown figure the point P is in first quadrant.

Option b :

(3, -1/4)

(-1/4)² = -36(3)

1/16 ≠ -108

The point (3, -1/4) is not on the parabola.

Option c :

(4, -4/9)

4² = -36(-4/9)

16 = 16

The point (4, -4/9) is on the parabola.

Option d :

The point (1, 1/36) is not on the parabola.

Option e :

 (6, -1)

6² = -36(-1)

36 = 36

The point (6, -1) is on the parabola.

Option f :

(2, -1/18)

2² = -36(-1/18)

4 ≠ 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.