IDENTIFY POINTS ON A COORDINATE PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
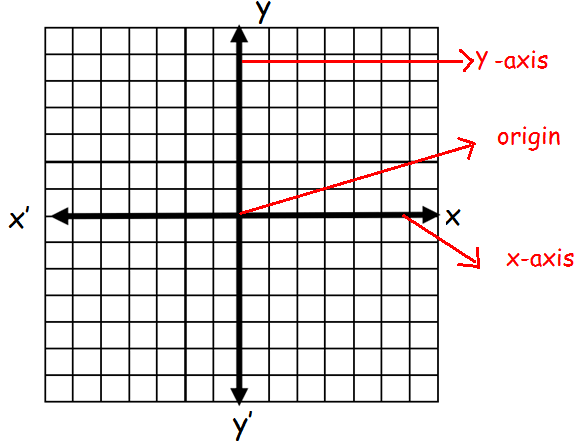
The coordinate plane is used to locate points. More precisely, points are located in reference to two perpendicular number lines called axes. The horizontal number line is the x-axis. The vertical number line is the y-axis.
- Points in the coordinate plane are named by ordered pairs of the form (x, y).
- The first number, or x-coordinate, corresponds to the numbers on the x-axis.
- The second number, or y-coordinate, corresponds to the numbers on the y-axis.
- The origin, labeled O, has coordinates (0, 0).
Coordinate Plane
Identifying Points on a Coordinate Plane
Example 1 :
Write the ordered pair for point G.
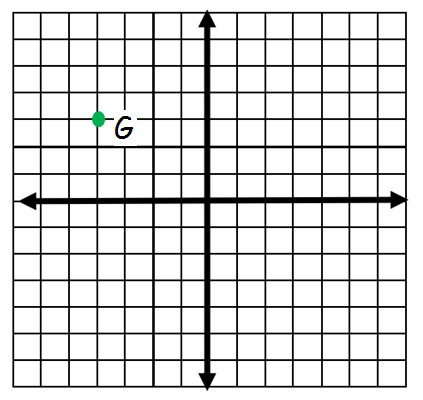
Solution :
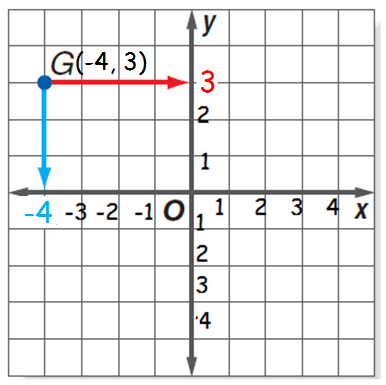
Follow along a vertical line through the point to find the x-coordinate on the x-axis. The x-coordinate is -4.
Follow along a horizontal line through the point to find the y-coordinate on the y-axis. The y-coordinate is 3.
So, the ordered pair for point G is (-4, 3). This can also be written as G(-4, 3).
Plotting a Point in a Coordinate Plane
The x-axis and y-axis separate the coordinate plane into four regions, called . Notice which quadrants contain positive and negative x-coordinates and which quadrants contain positive and negative y-coordinates. The axes are not located in any of the quadrants.
Signs of Ordered Pairs |
Quadrant | |
|
(+, +) (-, +) (-, -) (+, -) |
1st quadrant 2nd quadrant 3rd quadrant 4th quadrant |
When graphing an ordered pair, start at the origin. The x-coordinate indicates how many units to move right (positive) or left (negative). The y-coordinate indicates how many units to move up (positive) or down (negative).
|
If the x-coordinate value of the given point is 0, then the the given point will be located on y-axis. |
For example, the points (0, 3) and (0, -1) will be located on y-axis. | |
|
If the y-coordinate value of the given point is 0, then the the given point will be located on x-axis. |
For example, the points (5, 0) and (-2, 0) will be located on x-axis. |
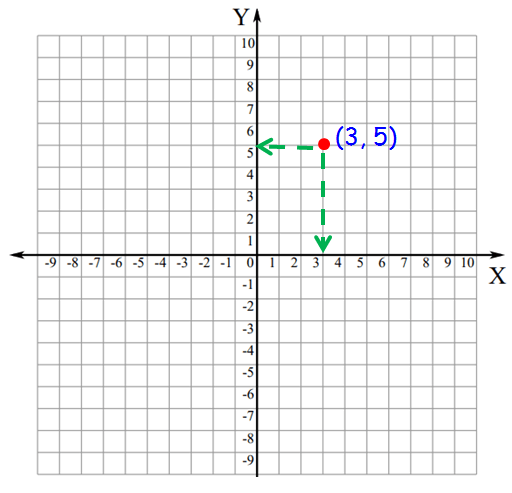
Example 2 :
Plot the given point on a coordinate plane.
A(3, 5)
Solution :
Both x and y-coordinate values are positive. So the given point will be located on the 1st quadrant.
Step 1 :
From origin, we have to move three units to the right side.
Step 2 :
Now move 4 units upward. .
Step 3 :
Draw a dot and label this point as (3, 5)
Example 3 :
Tell whether the statement is sometimes, always, or never true. Explain your reasoning.
a) The x-coordinate of a point on the x-axis is zero.
b) The y-coordinate of points in Quadrant III are positive.
c) The x-coordinate of a point in Quadrant II has the same sign as the y-coordinate of a point in Quadrant IV.
Solution :
a) The points on the x-axis will be in the form of (x, 0). Which shows the value of y must be 0. The given statement says its opposite. Then it is never true.
b) The points in the III quadrant will be in the form of (-x, -y). So, it is never true.
c) Sin of x-coordinate in quadrant II is negative. Sing of y-coordinate in quadrant IV is also negative. So, it is always true.
Example 3 :
Use the map of the Brevard Zoo in Melbourne, Florida.
a) Which exhibit is located at (2, 1)?
b) Name an attraction on the positive y-axis.
c) Is parking available in Quadrant II? If not, name a quadrant in which you can park.
d) Write two different ordered pairs that represent the location of La Selva Rainforest.
e) Which exhibit is closest to (−8, −3)?
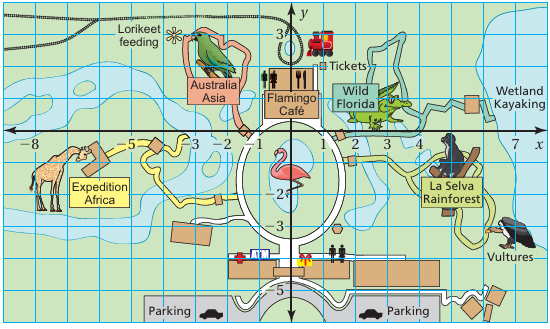
Solution :
Use the map of the Brevard Zoo in Melbourne, Florida.
a) At the point (2, 1) Wild Florida is located.
b) Australia Asia, Flamingo Cafe and Wild Florida are the attraction on the positive y-axis.
c) There is no parking in Quadrant II, but there are two parkings in quadrant III and IV.
d) (5, -2) and (4, -2) are the two different ordered pairs in La Selva Rainforest.
e) The exhibit Expedition Africa is closest to (−8, −3).
Example 4 :
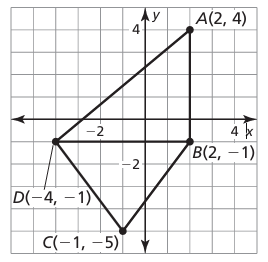
a) Find the area of ABD
b) Find the area of BCD
Solution :
a) Area of triangle ABD :
Base = 6 units and height = 5 units
Area of triangle = (1/2) x base x height
= (1/2) x 6 x 5
= 15 square units.
b) Area of triangle BCD :
base = 6 units and height = 4 units
Area of triangle = (1/2) x 6 x 4
= 12 square units.
Example 5 :
Name the ordered pair that is 5 units right and 2 units down from (−3, 4).
Solution :
Current location is (-3, 4),
- by moving 5 units right, -3 + 5 ==> 2
- by moving 2 units down, 4 - 2 ==> 2
After this process we get (2, 2).
Example 5 :
Describe and correct the error in the solution.

Solution :
From (0, 0),
- moving 5 units right 0 + 5 ==> 5
- moving 4 units up 0 + 4 ==> 4
After this process we get (5, 4). But the given point is (4, 5) and that is the error.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problems on Exponents and Radicals
Feb 21, 26 08:28 PM
SAT Math Problems on Exponents and Radicals -
SAT Math Problems on Angles
Feb 21, 26 08:20 PM
SAT Math Problems on Angles -
Digital SAT Math Problems and Solutions (Part - 9)
Feb 21, 26 10:41 AM
Digital SAT Math Problems and Solutions (Part - 9)

