IDENTIFY PARTS OF AN EXPRESSION

In an algebraic expression, we may find the following three parts.

(i) Terms

(ii) Factors

(iii) Coefficients

What is term ?

A single variable or a constant or a combination of these as a product or quotient forms a term.

Examples of terms :

5, -a, 3ab, 21/7, ........... etc

Terms can be added or subtracted to form an expression.

What is factor ?

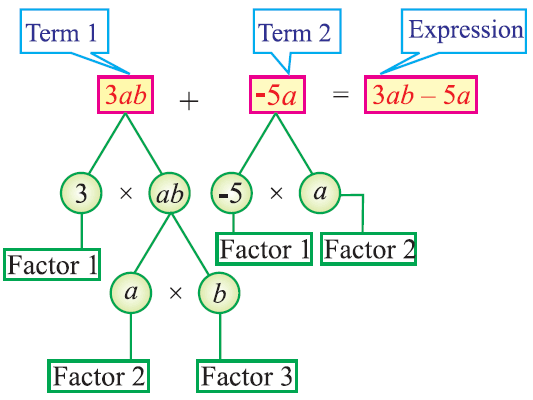
Consider the expression 3ab – 5a. It has two terms 3ab and -5a. The term 3ab is a product of factors 3, a and b. The term -5a is a product of -5 and a. The coefficient of a variable is a factor or factors.

Example :

In the term 3ab;

(i) the coefficient of ab is 3 (ii) the coefficient of a is 3b

(iii) the coefficient of b is 3a.

In the term –5a the coefficient of a is –5

What is constant ?

A number which is not having any variable with it is known as constant.

Identifying Parts of an Expression Using Flow Chart

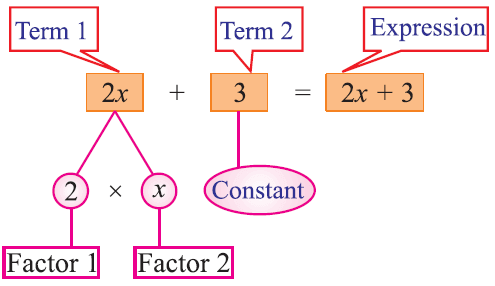
Example 1 :

Identify the parts of the following expression

2x + 3

Solution :

In the expression 2x + 3 the term 2x is made of 2 factors and 2 and x while 3 is a single factor.

Example 2 :

Identify the parts of the following expression

3ab - 5a

Solution :

Example 3 :

Identify the number of terms and coefficient of each term in the expression.

x²y² -  5x²y + (3/5)xy² - 11

Solution :

In the given expression, we have four terms.

Term 1  ==>  x²y²

Term 2  ==>  -5x²y

Term 3  ==>  (3/5)xy²

Term 4  ==>  -11

Coefficient of 1^st term  =  1

Coefficient of 2^nd term  =  -5

Coefficient of 3^rd term  =  3/5

Since the last term is not having any variable, it is a constant term.

Example 4 :

Identify the number of terms, coefficient and factors of each term in the expression.

3abc - 5ca

Solution :

The given expression contains two terms.

Term 1  ==> 3abc

Term 2 ==>  -5ca

Example 5 :

Identify the number of terms, coefficient and factors of each term in the expression.

1 + x + y²

Solution :

The given expression contains three terms.

Term 1  ==> 1

Term 2 ==>  x

Term 2 ==>  y²

Example 6 :

Identify the number of terms, coefficient and factors of each term in the expression.

3x²y² - 3xyz + z³ 

Solution :

The given expression contains three terms.

Term 1  ==> 3x²y²

Term 2 ==>  -3xyz 

Term 2 ==>  z³ 

Example 7 :

The coefficient of x⁴ in -5x⁷ + (3/7)x⁴ - 3x³ + 7x² - 1  

Solution :

The coefficient of x⁴ is 3/7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.