IDENTIFY LINEAR AND NONLINEAR FUNCTIONS

Determine whether each table represents a linear or nonlinear function.

Example 1 :

Solution :

In the above table, as x increases by 2, y increases by 3. The rate of change is constant. So, the above table represents a linear function.

Example 2 :

Solution :

In the above table, as x increases by 2, y increases by a greater amount each time. The rate of change is NOT constant. So, the above table represents a nonlinear function.

Example 3 :

Solution :

In the above table, as x increases by 3, y increases by a greater amount each time. The rate of change is NOT constant. So, the above table represents a nonlinear function.

Example 4 :

Solution :

In the above table, as x increases by 4, y decreases by 2 each time. The rate of change is constant. So, the above table represents a linear function.

Determine whether each graph represents a linear or nonlinear function.

Example 5 :

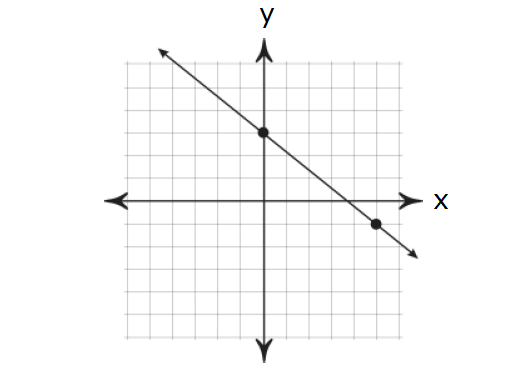
Solution :

The above graph is a straight line. So it represents a linear function.

Example 6 :

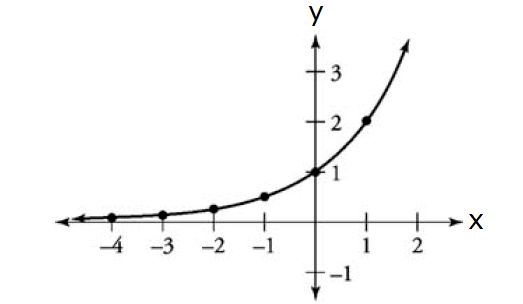
Solution :

The above graph is not a straight line. So it represents a nonlinear function.

Example 7 :

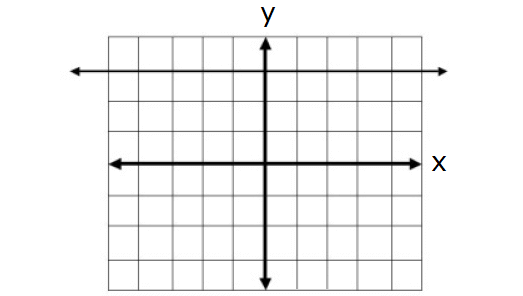
Solution :

The above graph is a straight line. So it represents a linear function.

Example 8 :

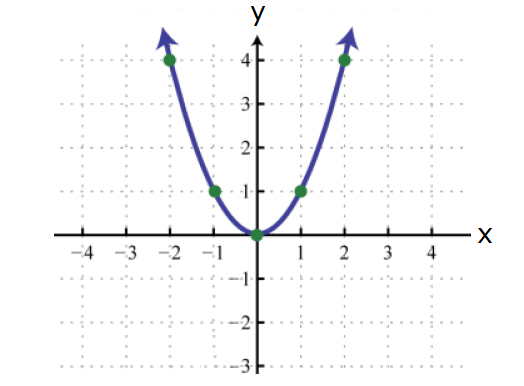
Solution :

The above graph is not a straight line. So it represents a nonlinear function.

Determine whether each equation represents a linear or nonlinear function. Remember that all linear functions can be written in the slope-intercept form, that is y = mx + b.

Example 8 :

y = 5x + 2

Solution :

The above function is in slope-intercept form.

So, it represents a linear function.

Example 9 :

y = 3(x - 4)

Solution :

The above function can be written in slope-intercept form.

y = 3(x - 4)

y = 3x - 12

So, it represents a linear function.

Example 10 :

y = x/2 + 5 

Solution :

The above function can be written in slope-intercept form.

y = x/2 + 5 

y = (1/2)x + 5

y = 0.5x + 5

So, it represents a linear function.

Example 11 :

y = 2/x - 3 

Solution :

The above function cannot be written in slope-intercept form.

So, it represents a nonlinear function.

Example 12 :

y = -5x 

Solution :

y = -5x

y = -5x + 0

The above function is in slope-intercept form.

So, it represents a linear function.

Example 13 :

Which equation represents a nonlinear function?

a) y = 4.7      b) y = 4 — x     c) y = π x       d) y = 4(x − 1)

Solution :

The equations y = 4.7, y = π x, and y = 4(x − 1) can be rewritten in slope-intercept form. So, they are linear functions. The equation y = 4 — x cannot be rewritten in slope-intercept form.

So, it is a nonlinear function. The correct answer is C

Example 14 :

Describe the difference between a linear function and a nonlinear function.

Solution :

The graph of a linear function shows a constant rate of change. A nonlinear function does not have a constant rate of change. So, its graph is not a line.

Example 15 :

Which one does not belong to  Which equation does not belong with the other three? Explain your reasoning.

a)  5y = 2x   b)  y = (2/5)   x    c)  10y = 4x    d)  5xy = 2

Solution :

a)  5y = 2x

Linear function in two variables x and y.

b)  y = (2/5)  x

Linear function in one variable.

c)  10y = 4x

Linear function in two variables x and y.

d)  5xy = 2

This is not a linear function. So, option d does not belong to the remaining.

Example 16 :

Does the equation represent a linear or nonlinear function? Explain.

a) 2x + 3y = 7

b) y + x = 4x + 5

c)  y = 8/x²

Solution :

a) 2x + 3y = 7

Linear function in two variables.

b) y + x = 4x + 5

y + x - 4x - 5 = 0

y - 3x - 5 = 0

Linear function in two variables.

c)  y = 8/x²

Since the variable is not at the numerator it is not a linear function. It is non linear function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.