IDENTIFY AND CLASSIFY POLYGONS

A polygon is any 2-dimensional closed shape formed by three or more line segments. Triangle is a polygon with least number sides, that is three.

If the shape had curves or didn't fully connect, then it can't be called a polygon.

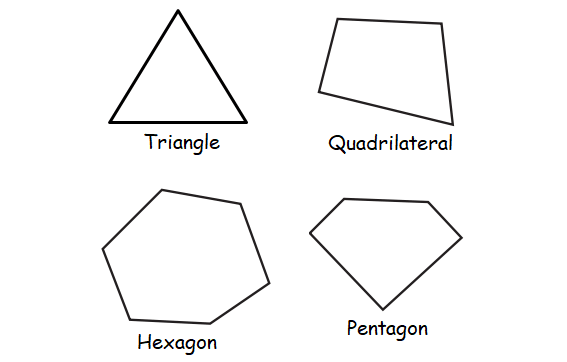
 A polygon can be identified and classified by the number of sides they have.

Note :

A polygon with more than 10 sides will be named as n-gon.

Examples : 

11-gon

12-gon

13-gon

Quadrilaterals

A polygon formed by four line segments is called a quadrilateral.

The sum of all the four angles of a quadrilateral is 360°.

Quadrilaterals with certain properties are given additional names. A trapezoid has exactly 1 pair of parallel sides. A parallelogram has 2 pairs of parallel sides. A rectangle has 4 right angles. A rhombus has 4 congruent sides. A square has 4 congruent sides and 4 right angles.

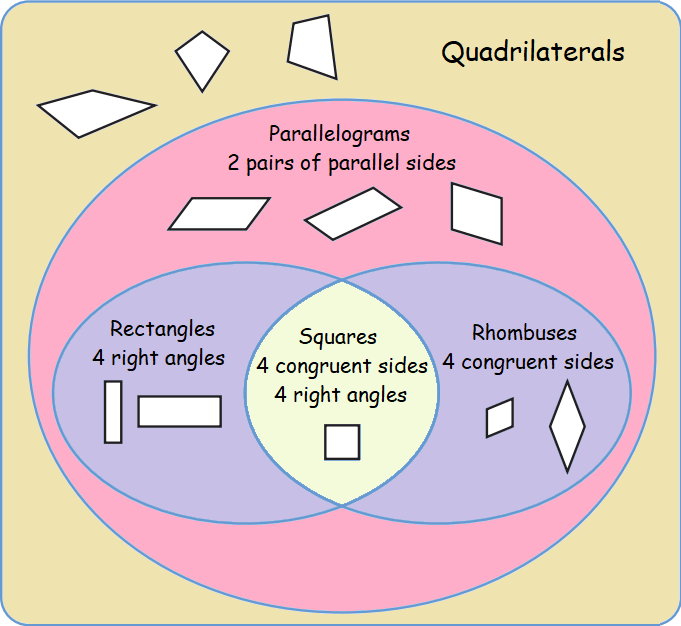
Parallelogram

If the opposite sides of a quadrilateral are parallel, then it is a parallelogram.

In a parallelogram,

• Opposite sides are parallel and equal.
• Opposite angles are equal and sum of any two adjacent angles is 180°
• Diagonals bisect each other.

Rectangle

A rectangle is a quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal.

Square

A square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle in which two adjacent sides have equal length. A square with vertices ABCD would be denoted ABCD

Rhombus

A rhombus is a simple quadrilateral whose four sides all have the same length.

• All sides are equal and opposite sides are parallel
• Opposite angles are equal and sum of any two adjacent angles is 180°.
• Diagonals bisect each other at right angles.

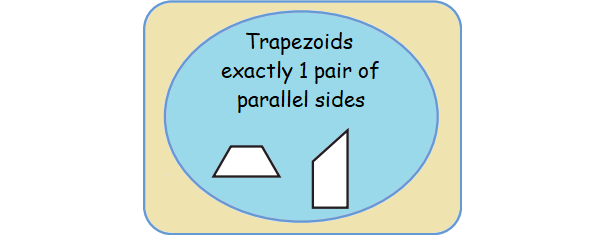
Trapezoid

Sides : One pair of opposite sides is parallel.

Angles : The angles at the ends of each non-parallel side are supplementary.

Diagonals : Diagonals need not be equal.

Isosceles Trapezoid 

Sides : One pair of opposite sides is parallel, the other pair of sides is equal in length.

Angles : The angles at the ends of each parallel side are equal.

Diagonals : Diagonals are equal in length.

Practice Questions

Problem 1 :

Complete each statement with always, sometimes, or never. Explain your reasoning.

a)  A square is _________ a rhombus.

b) A rectangle is _________ a square.

c) A rectangle _________ has congruent diagonals.

d)  The diagonals of a square _________ bisect its angles.

e)  A rhombus _________ has four congruent angles.

f)  A rectangle _________ has perpendicular diagonals.

Solution :

a)  A square is always a rhombus.

In square and in rhombus, all four sides will be equal. To rhombus become a square, each vertex angle should be 90 degree.

b) A rectangle is sometimes a square.

In rectangle opposite sides will be equal, in square all four sides will be equal. 

c) Since the diagonal is dividing the rectangle into two congruent triangles, their diagonals will also be equal.

A rectangle always has congruent diagonals.

d)  The diagonals of a square always bisect its angles.

e)  A rhombus always has four congruent angles.

The opposite angles are equal in rhombus. 

f)  A rectangle sometimes has perpendicular diagonals.

Problem 2 :

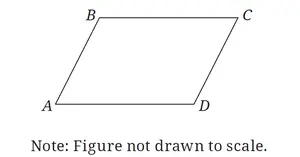
For what values of x and y is quadrilateral ABCD a parallelogram? Explain your reasoning.

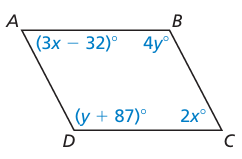
Solution :

Since it is parallelogram, the opposite sides are equal and parallel. 

Sum of co-interior angles = 180 degree

3x - 32 + y + 87 = 180

3x + y + 55 = 180

3x + y = 180 - 55

3x + y = 125 -----(1)

2x + 4y = 180

x + 2y = 90 ------(2)

2(3x + y) - (x + 2y) = 2(125) - 90

6x + 2y - x - 2y = 250 - 90

5x = 160

x = 160/5

x = 32

Applying x = 32 in (2), we get

32 + 2y = 90 

2y = 90 - 32

2y = 58

y = 58

y = 29

State the theorem you can use to show that the quadrilateral is a parallelogram.

Problem 3 :

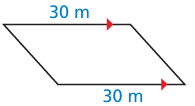
Solution :

Since opposite sides are equal, it must be a parallelogram.

Problem 4 :

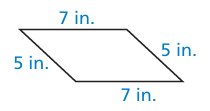
Solution :

Since opposite sides are equal, it must be a parallelogram.

Problem 5 :

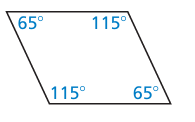
Solution :

Since opposite angles are equal, it must be a parallelogram.

Problem 6 :

For what value of x is quadrilateral MNPQ a parallelogram? Explain your reasoning.

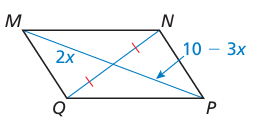
Solution :

In a parallelogram, the diagonals will be equal.

QN = MP

10 - 3x = 2x

10 = 2x + 3x

5x = 10

x = 10/5

x = 2

Problem 7 :

Find the measures of the numbered angles in rhombus ABCD.

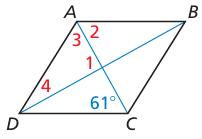
Solution :

In a rhombus, the diagonals will bisect each other at right angle.

<1 = 90 degree

In rhombus since opposite sides are parallel and equal, AC will be a transversal.

<2 = 61 (alternate interior angles)

61 + 2<3 + <2 = 180

61 + 2<3 + 61 = 180

122 + 2<3 = 180

2<3 = 180 - 122

2<3 = 58

<3 = 58/2

<3 = 29

<1 + <3 + <4 = 180

90 + 29 + <4 = 180

119 + <4 = 180

<4 = 180 - 119

<4 = 61

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.