HOW TO WRITE A DECIMAL IN EXPANDED FORM

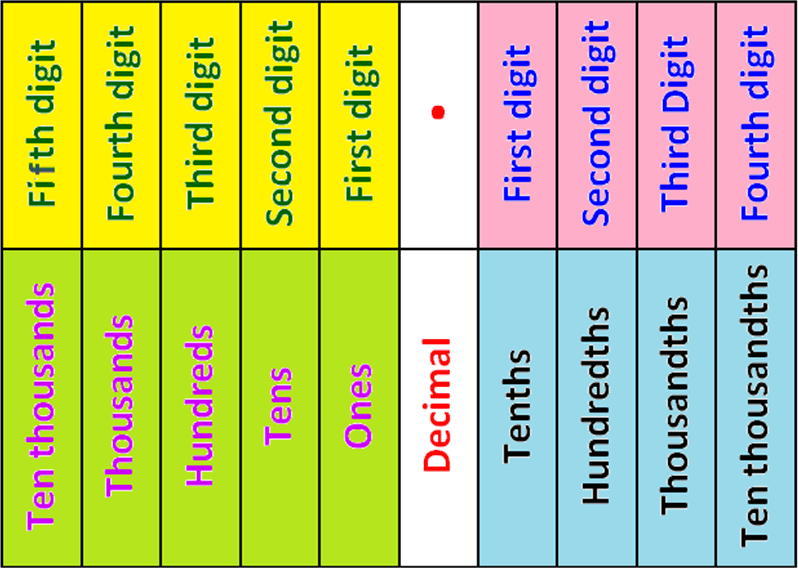
To write a decimal in expanded form, we have to break down down each digit according to its place value. We can start with the whole number portion, identifying the ten thusands, thousands, hundreds, tens, ones places. Then, move on to the tenths, hundredths, and thousandths and ten thousandths places.

Write the following decimals in expanded form :

Example 1 :

23.87

Solution :

= 23.87

Multiply each digit of 23.87 by its corresponding place value.

= 2x10 + 3x1 + 8x¹⁄₁₀ + 7x¹⁄₁₀₀

= 20 + 3 + ⁸⁄₁₀ + ⁷⁄₁₀₀

= 20 + 3 + 0.8 + 0.07

Example 2 :

7.8

Solution :

= 7.8

= 7x1 + 8x¹⁄₁₀

= 7 + ⁸⁄₁₀

= 7 + 0.8

Example 3 :

5.206

Solution :

= 5.206 

= 5x1 + 2x¹⁄₁₀ + 0x¹⁄₁₀₀ + 6x¹⁄₁₀₀₀

= 5 + ²⁄₁₀ + 0 + ⁶⁄₁₀₀₀

= 5 + 0.2 + 0.006

Example 4 :

1025.3

Solution :

= 1025.3

 = 1x1000 + 0x100 + 2x10 + 5x1 + 3x¹⁄₁₀

= 1000 + 0 + 20 + 5 + ³⁄₁₀

= 1000 + 0 + 20 + 5 + 0.3

Example 5 :

5.36

Solution :

= 5.36

 = 5x1 + 3x¹⁄₁₀ + 6x¹⁄₁₀₀

= 5 + ³⁄₁₀ + ⁶⁄₁₀₀

= 5 + 0.3 + 0.06

Example 6 :

0.389

Solution :

= 0.389 

= 3x¹⁄₁₀ + 8x¹⁄₁₀₀ + 9x¹⁄₁₀₀₀

= ³⁄₁₀ + ⁸⁄₁₀₀ + ⁹⁄₁₀₀₀

= 0.3 + 0.08 + 0.009

Example 7 :

0.0746

Solution :

= 0.0746 

= 7x¹⁄₁₀₀ + 4x¹⁄₁₀₀₀ + 6x¹⁄₁₀₀₀₀

= ⁷⁄₁₀₀ + ⁴⁄₁₀₀₀ + ⁶⁄₁₀₀₀₀

= 0.07 + 0.004 + 0.0006

Example 8 :

0.000043

Solution :

= 0.000043

 = 4x¹⁄₁₀₀₀₀₀ + 3x¹⁄₁₀₀₀₀₀₀

= ⁴⁄₁₀₀₀₀₀ + ³⁄₁₀₀₀₀₀₀

= 0.00004 + 0.000003

Example 9 :

2.4358 x 10²

Solution :

= 2.4358 x 10²

= 243.58

= 2x100 + 4x10 + 3x1 + 5x¹⁄₁₀ + 8x¹⁄₁₀₀

= 200 + 40 + 3 + ⁵⁄₁₀ + ⁸⁄₁₀₀

= 200 + 40 + 3 + 0.5 + 0.08

Example 10 :

9.57 x 10^-4

Solution :

= 9.57 x 10^-4

= 0.000957

= 9x¹⁄₁₀₀₀₀ + 5x¹⁄₁₀₀₀₀₀ + 7x¹⁄₁₀₀₀₀₀₀

= ⁹⁄₁₀₀₀₀ + ⁵⁄₁₀₀₀₀₀ + ⁷⁄₁₀₀₀₀₀₀

= 0.0009 + 0.00005 + 0.000007

Example 11 :

(1.78 x 10²) x (2.54 x 10¹)

Solution :

= (1.78 x 10²) x (2.54 x 10¹) 

= (1.78 x 2.54) x (10² x 10¹)

= 4.5212 x 10^{2 + 1}

= 4.5212 x 10³

= 4521.2

= 4x1000 + 5x100 + 2x10 + 1x1 + 2x¹⁄₁₀

= 4000 + 500 + 20 + 1 + ²⁄₁₀

= 4000 + 500 + 20 + 0.2

Example 12 :

(2.9375 x 10^-2) ÷ (1.25 x 10¹)

Solution :

= (2.9375 x 10^-2) ÷ (1.25 x 10¹)

= (2.9375 ÷ 1.25) x (10^-2 ÷ 10¹)

= 2.35 x 10^-2-1

= 2.35 x 10^-3

= 0.00235

= 2x¹⁄₁₀₀₀ + 3x¹⁄₁₀₀₀₀ + 5x¹⁄₁₀₀₀₀₀

= ²⁄₁₀₀₀ + ³⁄₁₀₀₀₀ + ⁵⁄₁₀₀₀₀₀

= 0.002 + 0.0003 + 0.00005

Example 13 :

(1.5 x 10^-2) + (2.3 x 10^-2)

Solution :

= (1.5 x 10^-2) + (2.3 x 10^-2)

Factor 10^-2.

= (1.5 + 2.3) x 10^-2

= 3.8 x 10^-2

= 0.038

= 3x¹⁄₁₀₀ + 8x¹⁄₁₀₀₀

= ³⁄₁₀₀ + ⁸⁄₁₀₀₀

= 0.03 + 0.008

Example 14 :

(2.9 x 10^-3) + (5.6 x 10^-1)

Solution :

= (2.9 x 10^-3) + (5.6 x 10^-2)

= (2.9 x 10^-3) + (56.0 x 10^-3)

Factor 10^-3.

= (2.9 + 56.0) x 10^-3

= 58.9 x 10^-3

= 0.0589

= 5x¹⁄₁₀₀ + 8x¹⁄₁₀₀₀ + 9x¹⁄₁₀₀₀₀

= ⁵⁄₁₀₀ + ⁸⁄₁₀₀₀ + ⁹⁄₁₀₀₀₀

= 0.05 + 0.008 + 0.0009

Example 15 :

(8.4 x 10^-3) - (1.6 x 10^-3)

Solution :

= (8.4 x 10^-3) - (1.6 x 10^-3)

Factor 10^-3.

= (8.4 - 1.6) x 10^-3

= 6.8 x 10^-3

= 0.0068

= 6x¹⁄₁₀₀₀ + 8x¹⁄₁₀₀₀₀

= ⁶⁄₁₀₀₀ + ⁸⁄₁₀₀₀₀

= 0.006 + 0.0008

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.