HOW TO TELL IF A TRIANGLE HAS ONE TWO OR NO SOLUTIONS

When solving a triangle, you must analyse the given information to determine if a solution exists. If you are given the measures of two angles and one side (ASA), then the triangle is uniquely defined. However, if you are given two sides and an angle opposite one of those sides (SSA), the ambiguous case may occur. In the ambiguous case, there are three possible outcomes:

No triangle exists that has the given measures; there is no solution
One triangle exists that has the given measures; there is one solution
Two distinct triangles exist that have the given measures; there are two distinct solutions.

For the ambiguous case in triangle ABC, when ∠A is an acute angle:

a ≥ b one solution
a = h one solution
a < h no solution,
b sin A < a < b two solutions

Where h = b sin A

For the ambiguous case in triangle ABC, when ∠A is an obtuse angle:

a ≤ b no solution
a > b one solution

Question :

For each triangle, determine whether there is no solution, one solution, or two solutions.

a) In triangle ABC, ∠A = 39°, a = 10 cm, and b = 14 cm.

Solution :

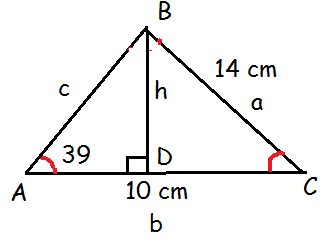
a/sin A = b/ sin B = c/sin C

14/sin 39 = 10/sin B = c/sin C

14/0.6293 = 10/sin B

22.24 = 10/sin B

sin B = 10/22.24 = 0.4496

B = 27 (approximately)

<A + <B + <C = 180

39 + 27 + <C = 180

<C = 180 - 66

<C = 114

sin A = Opposite side / Hypotenuse side

sin 39 = h/c

h = c sin 39

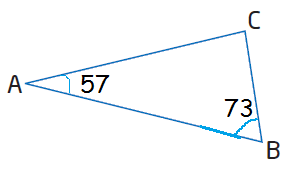
AB = c = 24 cm, BC = a, AC = b, <A = 57 and <B = 73

In triangle ABC,

<A + <B + <C = 180

57 + 73 + <C = 180

<C = 180 - 130 = 50

Using sin formula,

a/sin A = b/sin B = c/sin C

a/sin 57 = b/sin 73 = 24/sin 50

We have to solve for b.

Equating 1 and 3, we get

b/sin 73 = 24/sin 50

b/0.9563 = 24/0.7660

b = 31.33(0.9563)

b = 29.96

b = 30 cm (approximately)

Hence the indicated side is 30 cm.

b) In triangle ABC, ∠B = 38°, ∠C = 56°, and BC = 63 cm. Find the length of AB.

Solution :

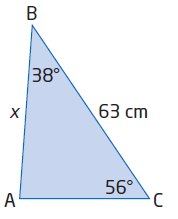
AB = c, BC = a = 63, AC = b, <C = 56 and <B = 38

In triangle ABC,

<A + <B + <C = 180

<A + 38 + 56 = 180

<A = 180 - 94 = 86

Using sin formula,

a/sin A = b/sin B = c/sin C

63/sin 86 = b/sin 38 = c/sin 56

We have to solve for c.

Equating 1 and 3, we get

63/sin 86 = c/sin 56

63/0.9975 = c/0.8290

63.15 = c/0.8290

c = 63.15(0.8290)

c = 52.35

c = 52.4 cm (approximately)

Hence the indicated side is 52.4 cm.

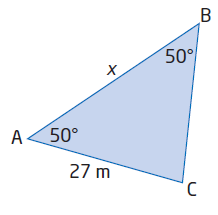
c) In triangle ABC, ∠A = 50°, ∠B = 50°, and AC = 27 m. Find the length of AB.

Solution :

AB = c, BC = a = 27 m, AC = b = 27 m, <A = 50 and <B = 50

In triangle ABC,

<A + <B + <C = 180

50 + 50 + <C = 180

<C = 180 - 100 = 80

Using sin formula,

a/sin A = b/sin B = c/sin C

27/sin 50 = 27/sin 50 = c/sin 80

We have to solve for c.

Equating 1 and 3, we get

27/sin 50 = c/sin 80

27/0.7660 = c/0.9848

35.24 = c/0.9848

c = 35.24(0.9848)

c = 34.70 m

Hence the indicated side is 34.7 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO TELL IF A TRIANGLE HAS ONE TWO OR NO SOLUTIONS

Recent Articles

Digital SAT Math Problems and Solutions (Part - 158)

Digital SAT Math Problems and Solutions (Part - 157)

AP Calculus AB Problems with Solutions (Part - 21)