HOW TO TELL IF A GRAPH REPRESENTS A FUNCTION

Question 1 :

Determine whether the graph given below represent functions. Give reason for your answers concerning each graph.

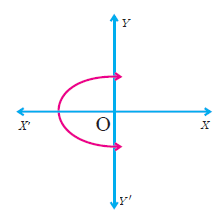
Solution :

Since the graph intersects the vertical line (y-axis) at two points, it is not a function.

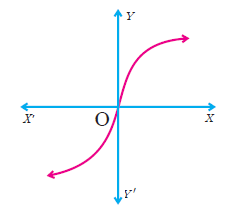
Solution :

The given graph intersects the vertical line (y-axis) at one point. It is a function.

(iii)  

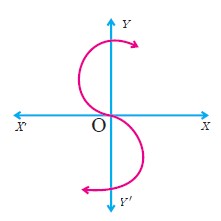
Solution :

The graph intersects the y-axis at three points, hence it is not a function.

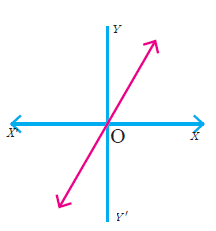
Solution :

The graph intersects the vertical line at most one point. Hence it is a function.

Question 2 :

Let f : A -> B be a function defined by f (x) =  (x/2) - 1 where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9} .

Represent f by 

(i) set of ordered pairs; (ii) a table; (iii) an arrow diagram; (iv) a graph

Solution :

(i) set of ordered pairs

f (x) =  (x/2) - 1

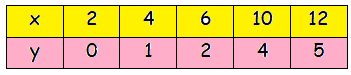
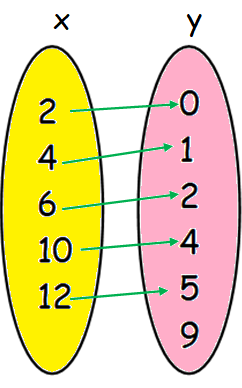
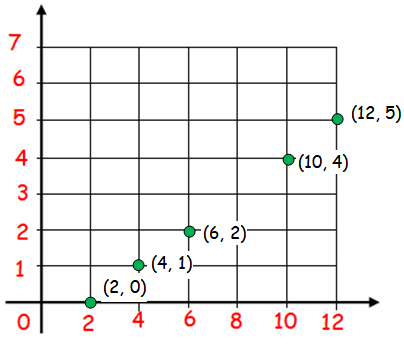
Set of ordered pairs  = {(2, 0) (4, 1) (6, 2) (10, 4) (12, 5)}

(ii) a table

(iii) an arrow diagram;

(iv) a graph

Question 3 :

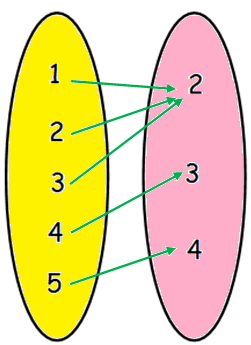
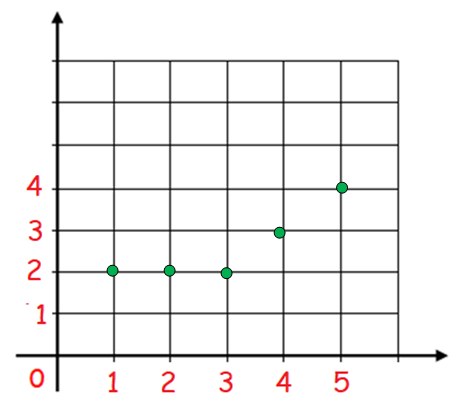
Represent the function f = {(1, 2),(2, 2),(3, 2),(4, 3),(5, 4)} through (i) an arrow diagram (ii) a table form (iii) a graph

Solution :

(i) an arrow diagram 

(ii) a table form

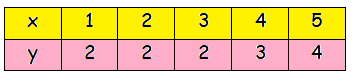
(iii) a graph

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.