HOW TO SOLVE TRIGONOMETRY WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To know, how to solve trigonometry word problems, we have to know the following basic things in trigonometry.
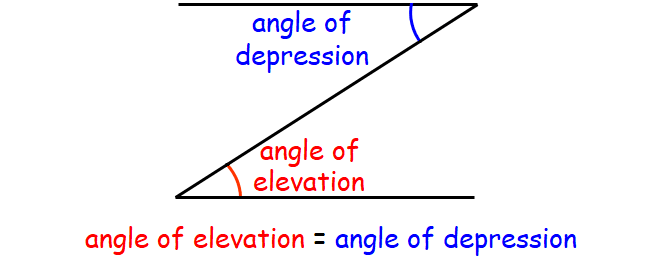
Angle of Elevation and Angle of Depression
Trigonometric Ratios
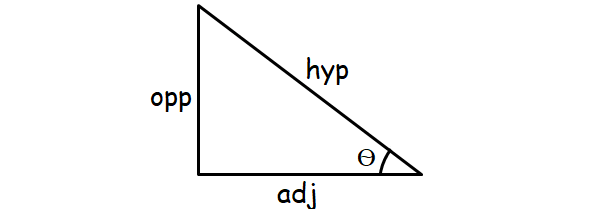
sinθ = opp/hyp
cosθ = adj/hyp
tanθ = opp/adj
opp ----> opposite side
hyp ----> hypotenuse
adj ----> adjacent side
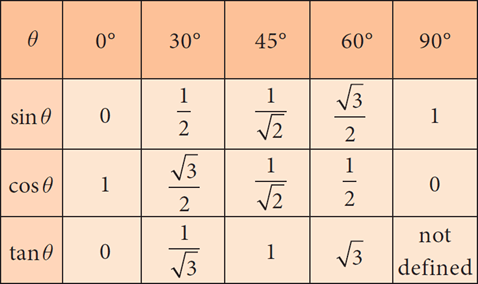
Trigonometric ratios of angles 0°, 30°, 45°, 60° and 90°.
Example 1 :
A student stands on the ground at point, which is 10m away from the foot of a pole. He observes the top of the pole at an angle of 60°. Suppose that the height of his eye level from the ground level is 1.2 m , Find the height of the pole.
Solution :
Step 1 :
Let us go through and understand the given information. From our understanding of the information given, we can draw the below picture.
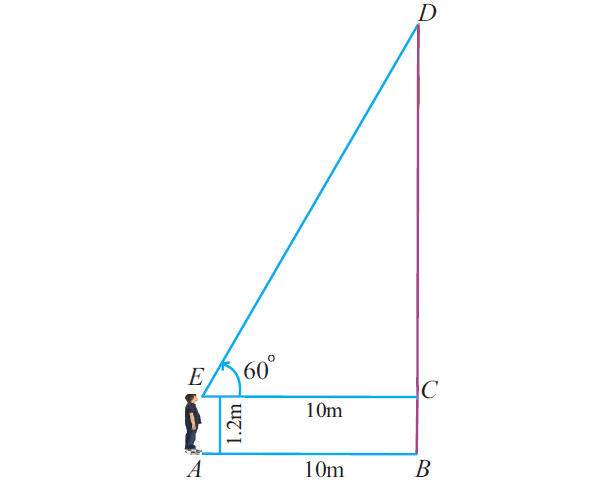
Step 2 :
In the picture drawn above, we have to give name for each position using English alphabets.
That is,
Student position ---> A
Foot of the pole ---> B
Student's eye level ---> E
Top of the pole ---> D
Point on the pole corresponding to eye level ---> C
Now, from the above figure, clearly height of the pole is BD.
And also,
BD = BC + CD
In the picture above, we have
AE = BC
AE = 1.2 m
So, BC = 1.2 m.
Step 3 :
Now, our aim is to get the length of CD.
Once CD is known, easily we can get the length of BD using BD = BC + CD.
Step 4 :
In the right angle triangle CDE, clearly CD is opposite side and EC is adjacent side and it is known to be 10m.
Step 5 :
In the right angle triangle CDE, we have to find the length of opposite side (CD) and the known side is adjacent side (EC = 10m).
Step 6 :
In this problem, we have to use the trigonometric ratio in which we have opposite side and adjacent side. Because, the length of adjacent side (EC = 10m) is known and we have to find the length of opposite side (CD).
Step 7 :
We can use the trigonometric ratio "tan" in this problem. Because, only in "tan", we have opposite side and adjacent side. Now, lets look at, how to find the length of CD.
Step 8 :
tan60° = opp/adj
√3 = CD/EC
√3 = CD/10
10√3 = CD
10 ⋅ 1.732 = CD
17.32 = CD
Step 9 :
The length of the pole BD = BC + CD
BD = 1.2 + 17.32
BD = 18.52
So, the length of the pole is 18.52 m.
Problem 2 :
A ladder 4.1 m in length rests against a vertical wall and reaches 3.5 m up from the ground level. Find
a) the angle the ladder makes with the ground.
b) the distance from the foot of the ladder to the wall.
Solution :
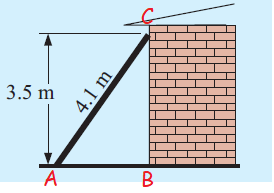
AC = 4.1 m
BC = 3.5 m
AB = x
|
sin θ = BC/AC sin θ = 3.5/4.1 sin θ = 0.853 θ = sin -1(0.853) = 58.53 |
cos θ = AB/AC cos (58.53) = AB/4.1 0.522 = AB/4.1 AB = 0.522(4.1) = 2.14 m |
The required angle is 58.53. So, the distance of ladder from the foot of the wall is 2.14 m.
Problem 3 :
From a point A, 30 m from the base of building B, the angle of elevation the top of the building C is 56 degree and to the top of the flag pole CD is is 60 degree.
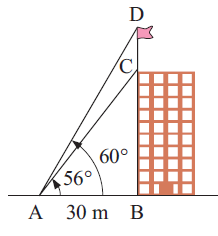
Find the length of the flag pole.
Solution :
In triangle ABC,
AB = 30 m
tan 56 = BC/AB
tan 56 = BC/30
BC = 30 (tan 56)
= 30(1.482)
= 44.46 m
In triangle ABD,
tan 60 = BD/AB
1.732 = (BC + CD)/30
1.732 = (44.46 + CD) / 30
44.46 + CD = 30(1.732)
44.46 + CD = 51.96
CD = 51.96 - 44.46
CD = 7.5 m
So, the length of the flag pole is 7.5 m.
Problem 4 :
The angle of elevation from a point on level ground to the top of the building 100 m high is 22 degree.
a) Find the distance of the point from the base of the building.
b) The distance the point must be moved towards the building in order that the angle of elevation becomes 40 degree.
Solution :
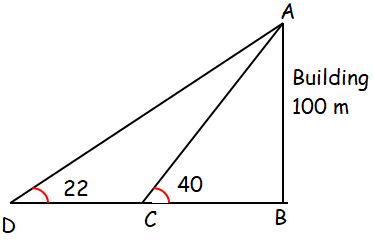
Distance moved = DC
In triangle ABC,
tan 40 = AB/BC
0.839 = 100 / BC
BC = 100/0.839
BC = 119.18
In triangle ABD,
tan 22 = AB/(BC + CD)
0.404 = 100/(119.18 + CD)
119.18 + CD = 100/0.404
119.18 + CD = 247.52
CD = 247.52 - 119.18
CD = 128.34 m
So, the distance moved is 128.34 m.
Problem 5 :
From the vertical cliff 80 m above sea level a fishing boat is observed at an angle of depression is 6 degree. How far out to sea is the boat ?
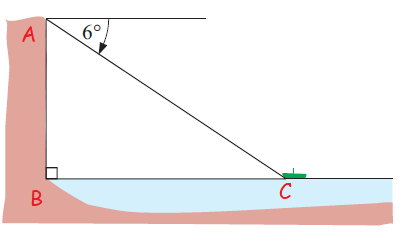
Solution :
<BCA = 6 degree
AB = 80 m
tan 6 = AB/BC
tan 6 = 80/BC
BC = 80/tan 6
= 80/0.105
BC = 761.1 m
So, the required distance is 761.1 m.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
GMAT Quantitative Reasoning Questions and Answers
Dec 27, 25 09:33 PM
GMAT Quantitative Reasoning Questions and Answers -
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41)

