HOW TO SOLVE TRIGONOMETRIC EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Solving trigonometrical equations is nothing but finding all replacements for the variable θ that make the equations true.
A solution of a trigonometrical equation is the value of the unknown angle that satisfies the equation. A trigonometrical equation may have infinite number of solutions.
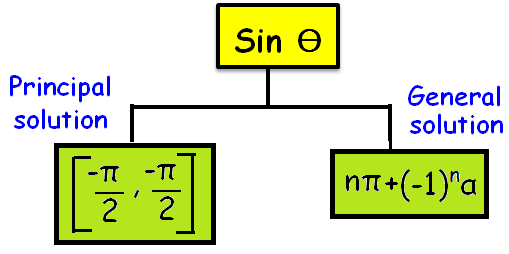
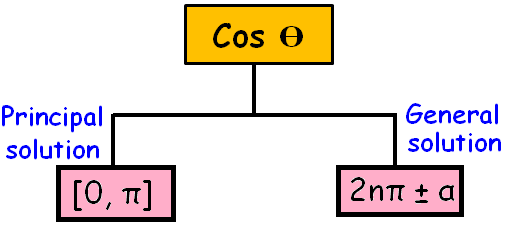
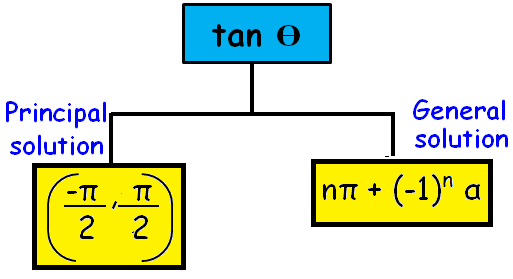
Principal Solution :
The solution in which the absolute value of the angle is the least is called principal solution.
General Solution :
The expression involving integer ‘n’ which gives all solutions of a trigonometrical equation is called the general solution.
Example 1 :
Solve : 2cos2θ + 3sinθ = 0.
Solution :
2cos2θ + 3sinθ = 0
First we have to convert the given function in one trigonometric ratio.
cos2θ = 1 - sin2θ
2(1 - sin2θ) + 3sinθ = 0
2 - 2sin2θ + 3sinθ = 0
Multiply the whole equation by (-)
2sin2θ - 3sinθ - 2 = 0
2sin2θ - 4sinθ + sinθ - 2 = 0
2sinθ(sinθ - 2) + 1(sinθ - 2) = 0
(2sinθ + 1) (sinθ - 2) = 0
|
2sinθ + 1 = 0 Subtract 1 on both sides 2sinθ + 1 - 1 = 0 - 1 2sinθ = -1 Divide by 2 on both sides sinθ = -1/2 |
sinθ - 2 = 0 sinθ = 2 it is not possible |
sinθ = - sin(π/6)
sinθ = sin(-π/6)
[satisfies the condition sinθ = sinα]
So, α = θ = -π/6.
General angle for sin θ :
θ = nπ + (-1)ⁿ α [n ∈ z ]
θ = nπ + (-1)ⁿ (-π/6)
For example
if we put n = 1, we will get
θ = π + (-1)¹ (-π/6) ==> π -π/6 ==> 5π/6
Hence θ = -π/6, 5π/6, ..........
Example 2 :
Solve : 2tanθ - cotθ = -1
Solution :
2tanθ - cotθ = -1
2tanθ - (1/tanθ) = -1
(2tan2θ - 1)/tanθ = -1
Multiply by tanθ on both sides.
(2tan2θ - 1) = -tanθ
2tan2θ + tanθ - 1 = 0
Let x = tanθ
2x2 + x - 1 = 0
2x2 + 2x - x - 1 = 0
2x(x + 1) - 1(x + 1) = 0
(2x - 1)(x + 1) = 0
|
2x - 1 = 0 2tanθ - 1 = 0 Add 1 on both sides 2tanθ = 1 Divide by 2 on both sides tanθ = 1/2 |
x + 1 = 0 Subtract 1 on both sides x + 1 - 1 = 0 - 1 x = -1 tanθ = -1 |
tanθ = -1
tanθ = -tan(π/4)
tanθ = tan(-π/4)
[satisfies the condition tanθ = tanα]
So, α = θ = -π/4
General angle for tanθ :
θ = nπ + (-1)ⁿ α [n ∈ z ]
θ = nπ -(π/4)
tanθ = 1/2
θ = tan-1(1/2)
θ = nπ + (-1)ⁿ α [n ∈ z ]
θ = nπ + tan-1(1/2)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
