HOW TO SOLVE SYSTEMS OF LINEAR INEQUALITIES IN ONE VARIABLE

Example 1 :

Solve the following system of linear inequalities.

(5x/4) + (3x/8)  >  39/8

(2x - 1)/12 - (x - 1)/3  <  (3x + 1)/4

Solution :

Solving the first inequality : 

(5x/4) + (3x/8)  <  39/8

10x/8 + 3x/8  <  39/8

(10x + 3x)/8  <  39/8

13x/8  <  39/8

Multiply each side by 8.

13x  <  39

Divide each side by 13. 

x  <  3

Solution set for the first inequality is

(-∞, 3)

Sketch the graph :

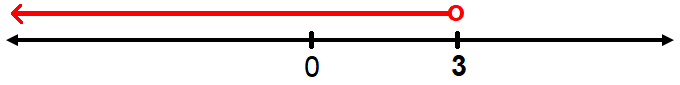
Solving the second inequality :

(2x - 1)/12 - (x - 1)/3  <  (3x + 1)/4

(2x - 1)/12 - 4(x - 1)/12  <  (3x + 1)/4

[(2x - 1) - 4(x - 1)]/12  <  (3x + 1)/4

[2x - 1 - 4x + 4]/12  <  (3x + 1)/4

(-2x + 3)/12  <  (3x + 1)/4

Multiply each side by 12. 

(-2x + 3)  <  3(3x + 1)

-2x + 3  <  9x + 3

Add 2x to each side.  

3  <  11x + 3

Subtract 3 from each side.

0  <  11x

Divide each side by 11.

0  <  x

So, the solution set for the second inequality is

(0, ∞)

Sketch the graph :

Combine the graphs of the solution sets of the first and second inequalities. 

In the above graph, the common region found in the solution sets of the first and second inequalities is 

(0, 3)

Therefore, the solution set for the given system of inequalities is

(0, 3)

Example 2 :

Solve the following system of linear inequalities 

x / (2x + 1)  ≥  1 / 4

6x / (4x - 1)  <  1 / 2 

Solution :

Solving the first inequality :

x / (2x + 1)  ≥  1 / 4

Multiply each side by 4(2x + 1).

4x  ≥  2x + 1

Subtract 2x from each side. 

2x  ≥  1

Divide each side by 2.

x  ≥  1 / 2

So, solution set for the first inequality is

[1/2, ∞)

Sketch the graph :

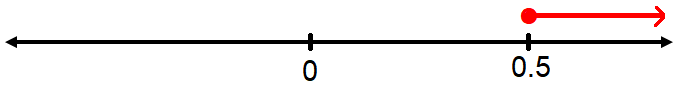
Solving the second inequality :

6x / (4x - 1)  <  1 / 2

Multiply each side by 2(4x - 1).

12x  <  4x - 1

Subtract 4x from each side. 

8x  <  - 1

Divide each side by 8.

x  <  - 1 / 8

So, the solution set for the second inequality is

(- ∞, - 0.125)

Sketch the graph :

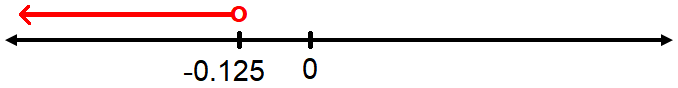
Combine the graphs of the solution sets of the first and second inequalities. 

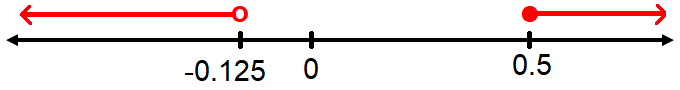
In the above graph, there is common region found in the solution sets of the first and second inequalities. 

Therefore, no solution for the given system of inequalities. 

Example 3 :

Solve the following system of linear inequalities 

3x - 6  ≥  0,  4x - 10  ≤  6

Solution :

Solving the first inequality : 

3x - 6  ≥  0

Add 6 to each side. 

3x  ≥  6

Divide each side by 3. 

x  ≥  2

So, the solution set for the first inequality is

[2, ∞)

Sketch the graph :

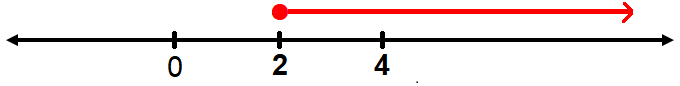
Solving the second inequality : 

4x - 10  ≤  6

Add 10 to each side. 

4x  ≤  16

Divide each side by 4. 

x  ≤  4

So, the solution set for the second inequality is

(-∞, 4]

Sketch the graph :

Combine the graphs of the solution sets of the first and second inequalities. 

In the above graph, the common region found in the solution sets of the first and second inequalities is 

[2, 4]

Therefore, the solution set for the given system of inequalities is

[2, 4]

Example 4 :

The tallest person who ever lived was approximately 8 feet 11 inches tall.

a. Write an inequality that represents the heights of every other person who has ever lived.

b. Is 9 feet a solution of the inequality? Explain.

Solution :

a) 

Let x be the height of the tallest person.

Converting 8 ft 11 inches into inches :

1 ft = 12 inches

8 ft = 8 x 12

= 96 inches

= 96 + 11

= 107 inches

x < 107

b) When 9 ft = 9 x 12

= 108 inches

Applying x = 108 inches

108 < 107

False. Then 9 ft is not a solution of the inequality.

Example 5 :

The area of the rectangle is greater than 60 square feet. Write and solve an inequality to find the possible values of x.

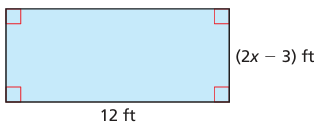
Solution :

Area of the rectangle > 60 square ft

Length = 12 ft and width = (2x - 3) ft

length • width > 60

12(2x - 3) > 60

24x - 36 > 60

24x > 60 + 36

24x > 96

x > 96/24

x > 4

Example 6 :

Forest Park Campgrounds charges a $100 membership fee plus $35 per night. Woodland Campgrounds charges a $20 membership fee plus $55 per night. Your friend says that if you plan to camp for four or more nights, then you should choose Woodland Campgrounds. Is your friend correct? Explain.

Solution :

Let x be the charge per night

Forest Park Campgrounds charges :

= 100 + 35x

Woodland Campgrounds charges :

= 200 + 55x

When number of nights is 4, then

Cost spent on forest park = 100 + 35(4)

= 100 + 140

= 240

Cost spent on woodland park = 20 + 55(4)

= 20 + 220

= 240

When number of nights is 5, then

Cost spent on forest park = 100 + 35(5)

= 100 + 175

= 275

Cost spent on woodland park = 20 + 55(5)

= 20 + 275

= 295

Your friend is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.