HOW TO SOLVE QUADRATIC INEQUALITIES STEP BY STEP

In this section, you will learn, how to solve quadratic inequalities in the form

ax² + bx + c < 0

ax² + bx + c ≤ 0

ax² + bx + c > 0

ax² + bx + c ≥ 0

(i) First solve ax² + bx + c = 0.

(ii) If there are no real solutions, then one of the above inequality holds for all x ∈ R

(iii) If there are real solutions, which are called critical points, then label those points on the number line.

(iv) Note that these critical points divide the number line into disjoint intervals. (It is possible that there may be only one critical point.)

(v) Choose one representative number from each interval.

(vi) Substitute that these representative numbers in the inequality.

(vii) Identify the intervals where the inequality is satisfied.

Example 1 :

Solve 2x² + x − 15 ≤ 0.

Solution :

First let us solve the given quadratic equation by factoring.

2x² + x − 15 = 0

2x² + 6x - 5x − 15 = 0

2x(x + 3) - 5(x + 3) = 0

(2x - 5) (x + 3) = 0

2x - 5 = 0 x + 3 = 0

2x = 5 x = -3

x = 5/2

The critical numbers are -3 and 5/2.

Now let us mark them in number line.

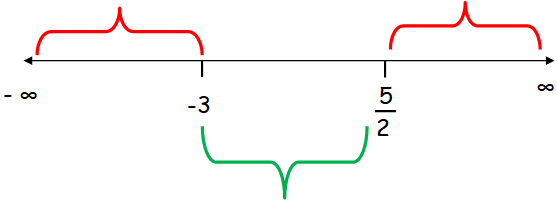
Applying any values within the interval, we get

Intervals	Signs of factors (2x-5)(x+3)	Sign of given inequality
(-∞, -3] say x = - 4	(-) (-)	+
[-3, 5/2] say x = 0	(-) (+)	-
[5/2, ∞) say x = 3	(+) (+)	+

From the above table, we come to know that the interval [-3, 5/2] satisfies the given inequality.

Hence, the solution is [-3, 5/2].

Example 2 :

Solve −x² + 3x − 2 ≥ 0.

Solution :

First let us solve the given quadratic equation by factoring.

The coefficient of x must be positive, so we have to multiply the inequality by negative.

x² - 3x + 2 ≤ 0

Multiply the equation by negative.

x² - 3x + 2 = 0

x² - 1x - 2x + 2 = 0

x (x - 1) - 2(x - 1) = 0

(x - 2) (x - 1) = 0

x - 2 = 0 x - 1 = 0

x = 2 x = 1

Writing them as intervals, we get

(-∞, 1] [1, 2] [2, ∞)

Applying any values within the interval, we get

Intervals	Signs of factors (x-2)(x-1)	Sign of given inequality
(-∞, 1] say x = 0	(-) (-)	+
[1, 2] say x = 1.5	(-) (+)	-
[2, ∞) say x = 3	(+) (+)	+

From the above table, we come to know that the interval [1, 2] satisfies the given inequality.

Hence, the solution is [1, 2].

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO SOLVE QUADRATIC INEQUALITIES STEP BY STEP

Recent Articles

Printable Math Worksheets

Printable Math Worksheets for Grade 2

Sequences and Series