HOW TO SOLVE QUADRATIC EQUATIONS BY FACTORING
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A quadratic polynomial is of the form of
ax2 + bx + c = 0
where a, b, c are real numbers.
What is factoring quadratics ?
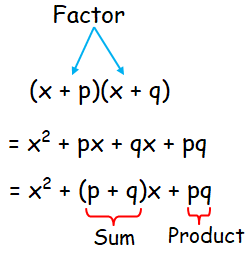
Factoring quadratics is a method of expressing the quadratic equation ax2 + bx + c = 0 as a product of its linear factors as (x - k)(x - h),
where h, k are the roots of the quadratic equation ax2 + bx + c = 0.
Factorise :
Problem 1 :
x2–7x – 8 = 0
Solution :
Step 1 :
Product of factors = -8
Sum of factors = -7
Step 2 :
Finding the factors of product and sum.
2 · 4 = 8 and 2 + 4 ≠ 6
-8 · 1 = -8 and -8 + 1 = -7
So, the factors are -8 and +1
Step 3 :
x2 + 1x – 8x – 8 = 0
By grouping,
(x2 + 1x) + (-8x – 8) = 0
Step 4 :
By taking the common factor, we get
x(x + 1) - 8(x + 1) = 0
(x – 8)(x + 1) = 0
Step 5 :
Equating each factors to zero.
x – 8 = 0 and x + 1 = 0
x = 8 and x = -1
Problem 2 :
x2 + 4x – 21 = 0
Solution :
Step 1 :
Product of factors = -21
Sum of factors = 4
Step 2 :
Finding the factors of product and sum.
1 · (-21) = -21 and 1 + (-21) ≠ -20
7 · (-3) = -21 and 7 + (-3) = 4
So, the factors are +7 and -3
Step 3 :
x2 + 7x – 3x – 21 = 0
By grouping,
(x2 + 7x) + (-3x – 21) = 0
Step 4 :
By taking the common factor, we get
x(x + 7) -3(x + 7) = 0
(x – 3)(x + 7) = 0
Step 5 :
Equating each factor to zero
x – 3 = 0 and x + 7 = 0
x = 3 and x = -7
Problem 3 :
x2 - x – 2 = 0
Solution :
Step 1 :
Product of factors = -2
Sum of factors = -1
Step 2 :
Finding the factors of product and sum.
2 · (-1) = -2 and 2 + (-1) ≠ 1
1 · (-2) = -2 and 1 + (-2) = -1
So, the factors are -2 and 1
Step 3 :
x2 + x – 2x – 2 = 0
By grouping,
(x2 + x) + (-2x – 2) = 0
Step 4 :
By taking the common factor, we get
x(x + 1) -2(x +
1) = 0
(x – 2)(x + 1) = 0
Step 5 :
Equating each factors to zero.
x – 2 = 0 and x + 1 = 0
x = 2 and x = -1
Problem 4 :
x2 - 2x – 8 = 0
Solution :
Step 1 :
Product of factors = -8
Sum of factors = -2
Step 2 :
Finding the factors of product and sum.
(-1) · 8 = -8 and -1 + 8 ≠ 7
(-4) · 2 = -8 and (-4) + 2 = -2
So, the factors are -4 and 2.
Step 3 :
x2 - 4x + 2x – 8 = 0
By grouping,
(x2 - 4x) + (2x – 8) = 0
Step 4 :
By taking the common factor, we get
x(x - 4) + 2(x - 4) = 0
(x + 2)(x - 4) = 0
Step 5 :
Equating each factors to zero.
x + 2 = 0 and x - 4 = 0
x = -2 and x = 4
Problem 5 :
x2 + 5x – 24 = 0
Solution :
Step 1 :
Product of factors = -24
Sum of factors = 5
Step 2 :
Finding the factors of product and sum.
(-6) · 4 = -24 and (-6) + 4 ≠ -2
8 · (-3) = -24 and 8 + (-3) = 5
So, the factors are 8 and -3
Step 3 :
x2 + 8x – 3x – 24 = 0
By grouping,
(x2 + 8x) + (-3x – 24) = 0
Step 4 :
By taking the common factor, we get
x(x + 8) -3(x + 8) = 0
(x – 3)(x + 8) = 0
Step 5 :
Equating each factors to zero.
x – 3 = 0 and x + 8 = 0
x = 3 and x = -8
Problem 6 :
x2 - 3x – 10 = 0
Solution :
Step 1 :
Product of factors = -10
Sum of factors = -3
Step 2 :
Finding the factors of product and sum.
(-1) · 10 = -10 and -1 + 10 ≠ 9
(-5) · 2 = -10 and (-5) + 2 = -3
So, the factors are -5 and +2
Step 3 :
x2 - 5x + 2x – 10 = 0
By grouping,
(x2 - 5x) + (2x – 10) = 0
By taking the common factor, we get
x(x - 5) + 2(x - 5) = 0
(x – 5)(x + 2) = 0
Equating each factors to zero.
x – 5 = 0 and x + 2 = 0
x = 5 and x = -2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


