HOW TO SOLVE A CUBIC EQUATION USING THE FACTOR THEOREM

Solve :

Problem 1 :

2x³ – x² – x = 0

Solution :

Let f(x) = 2x³ – x² – x

Using trial and error method.

 f(1) = 2(1)³ – (1)² – 1

= 2 – 1 – 1

= 2 - 2

f(1) = 0

Since f(1) = 0, x – 1 is a factor.

For the quadratic polynomial.

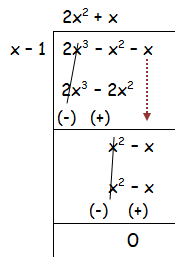
f(x) = (x – 1)(2x² + x)

(x – 1) x(2x + 1) = 0

Equating each factors to zero.

x – 1 = 0, x = 0 and 2x + 1 = 0

x = 1, x = 0 and 2x = -1

         x = -1/2

So, the solution of x is {1, 0, -1/2}.

Problem 2 :

x³ – x = 0

Solution :

Let f(x) = x³ - x

x(x² – 1) = 0

Equating each factors to zero.

x = 0 and (x² – 1) = 0

x² = 1

  x = ±1

So, the solution of x is {±1, 0}.

Problem 3 :

x³ + 3x² – 4x -12 = 0

Solution :

Let f(x) = x³ + 3x² – 4x - 12

 f(1) = (1)³ + 3(1)² – 4(1) - 12

= 1 + 3 – 4 - 12

 f(1) = -12 ≠ 0

f(-1) = (-1)³ + 3(-1)² – 4(-1) – 12

= -1 + 3 + 4 – 12

= 2 – 8

f(-1) = -6 ≠ 0

f(2) = (2)³ + 3(2)² – 4(2) – 12

= 8 + 12 – 8 – 12

f(2) = 0 

Since f(2) = 0, x – 2 is a factor.

For the quadratic factor.

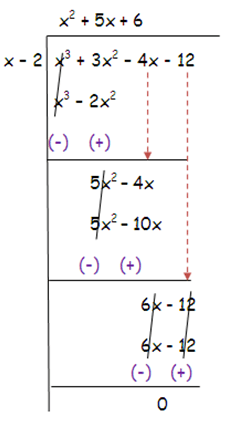
f(x) = (x – 2)(x² + 5x + 6)

By factoring quadratic polynomial, we get

(x – 2) (x² + 3x + 2x + 6) = 0

By grouping,

(x – 2) (x² + 3x) + (2x + 6) = 0

(x – 2) x(x + 3) + 2(x + 3) = 0

(x – 2)(x + 3)(x + 2) = 0

Equating each factors to zero.

x – 2 = 0, x + 3 = 0 and x + 2 = 0

x = 2, x = -3 and x = -2

So, the solution of x is {±2, -3}.

Problem 4 :

x³ – 3x – 2 = 0

Solution :

Let f(x) = x³ + 0x² – 3x – 2

 f(1) = (1)³ + 0(1)² – 3(1) - 2

= 1 – 3 – 2

= -2 - 2

f(1) = -4 ≠ 0

f(-1) = (-1)³ + 0(-1)² – 3(-1) - 2

= -1 + 3 – 2

= 2 - 2

f(-1) = 0

Since f(-1) = 0, x + 1 is a factor.

For the quadratic factor.

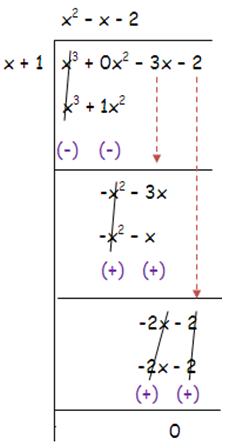
f(x) = (x + 1) (x² – x – 2)

By factoring quadratic polynomial, we get

(x + 1) (x² + x – 2x – 2) = 0

By grouping,

(x + 1) (x² + x) + (-2x – 2) = 0

(x + 1) x(x + 1) + (-2)(x + 1) = 0

(x + 1)(x + 1)(x - 2) = 0

Equating each factors to zero.

x + 1 = 0 and x – 2 =0

x = -1 and x = 2

So, the solution of x is {-1, 2}.

Problem 5 :

2x³ + 5x² – 14x – 8 = 0

Solution :

Let f(x) = 2x³ + 5x² – 14x – 8

Here,

f(1) = -15 ≠ 0

f(-1) = 9 ≠ 0

f(2) = 0

Since f(2) = 0, x - 2 is a factor.

For the quadratic factor.

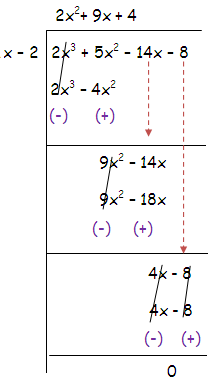
f(x) = (x – 2) (2x² + 9x + 4)

By factoring quadratic polynomial, we get

(x – 2) (2x² + x + 8x + 4) = 0

By grouping,

(x – 2) (2x² + x) + (8x + 4) = 0

(x – 2) x(2x + 1) + 4(2x + 1) = 0

(x – 2)(x + 4)(2x + 1) = 0

x – 2 = 0, 2x + 1 = 0 and x + 4 = 0

x = 2, x = -1/2 and x = -4

So, the solution of x is {2, -1/2, -4}.

Problem 6 :

x³ + 7x² – 36 = 0

Solution :

Let f(x) = x³ + 7x² + 0x – 36

Here,

f(1) = -28 ≠ 0

f(-1) = -30 ≠ 0

f(2) = 0

Since f(2) = 0, x – 2 is a factor.

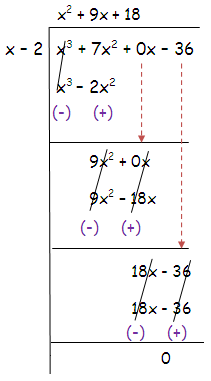
f(x) = (x – 2) (x² + 9x + 18)

(x – 2) (x² + 6x + 3x+ 18) = 0

By grouping,

(x – 2) (x² + 6x) + (3x + 18) = 0

(x – 2) x(x + 6) + 3(x + 6) = 0

(x – 2)(x + 3)(x + 6) = 0

x – 2 = 0, x + 3 = 0 and x + 6 = 0

x = 2, x = -3 and x = -6

So, the solution of x is {2, -3, -6}.

Problem 7 :

4x³ + 12x² + 9x + 2 = 0

Solution :

Let f(x) = 4x³ + 12x² + 9x + 2

Here,

f(1) = 27 ≠ 0

f(-1) = 1 ≠ 0

f(2) = 100 ≠ 0

f(-2) = 0

Since f(-2) = 0, x + 2 is a factor.

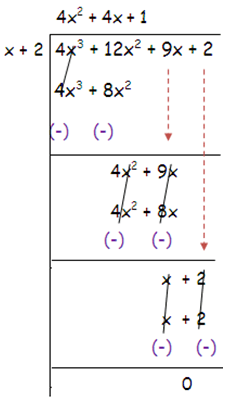
f(x) = (x + 2) (4x² + 4x + 1)

(x + 2) (4x² + 2x + 2x + 1) = 0

By grouping,

(x + 2) (4x² + 2x) + (2x + 1) = 0

(x + 2) 2x(2x + 1) + 1(2x + 1) = 0

(x + 2)(2x + 1) = 0

x + 2 = 0 and 2x + 1 = 0

x = -2 and x = -1/2

So, the solution of x is {-2, -1/2}.

Problem 8 :

x³ – 2x² – 4x + 3 = 0

Solution :

Let f(x) = x³ – 2x² – 4x + 3

Here,

Since f(3) = 0, x – 3 is a factor.

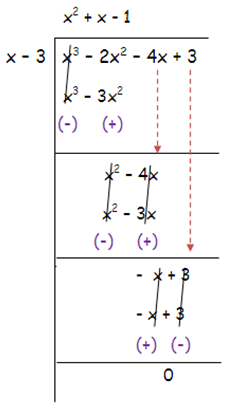
f(x) = (x – 3)(x² + x – 1)

(x – 3)(x² + x – 1) = 0

Since x² + x – 1 is not factorable, we use the quadratic formula.

x = -b ± √(b² – 4ac)/2a

Here a = 1, b = 1, and c = -1

= -1 ± √((-1)² – 4(-1)(1))/2(1)

= -1 ± √(1 + 4)/2

x = (-1 ± √5)/2

x = 3 and x = (-1 ± √5)/2

So, the solution of x is {3, (-1 ± √5)/2}.

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.