HOW TO SKETCH THE GRAPH OF THE FUNCTION IN THE GIVEN INTERVAL

Sketch the graph of each of the following functions on the interval [−1.3, 1.3].

Example 1 :

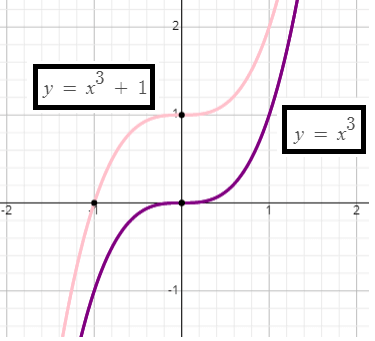
f(x) = x³ + 1

Solution :

For the given function f(x), the basic function is g(x) = x³.

Then, the given function can be written as

f(x) = g(x) + 1

So, there is a vertical translation of 1 unit up.

To get the graph of the given function f(x) on the interval [-1.3, 1.3], we have to shift the graph of the basic function g(x), verticaly up by 1 unit.

Example 2 :

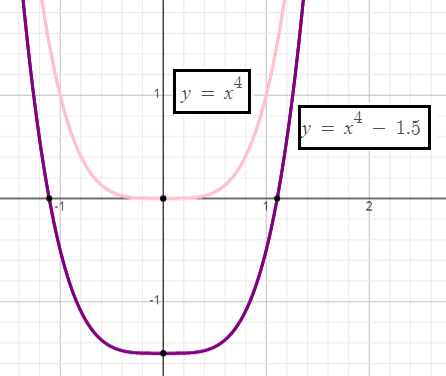
f(x) = x⁴ − 1.5

Solution :

For the given function f(x), the basic function is g(x) = x⁴.

Then, the given function can be written as

f(x) = g(x) - 1.5

So, there is a vertical translation of 1.5 units down.

To get the graph of the given function f(x) on the interval [-1.3, 1.3], we have to shift the basic function g(x) verticaly down by 1.5 units.

Example 3 :

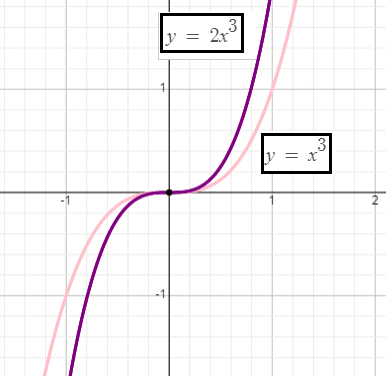
f(x) = 2x³

Solution :

For the given function f(x), the basic function is g(x) = x³.

Then, the given function can be written as

f(x) = 2g(x)

So, there is a vertical strech by a factor of 2.

To get the graph of the given function f(x) on the interval [-1.3, 1.3], we have to strech the basic function g(x) verticaly by a factor of 2. That is, y-coordinate of each point on the basic function has to be multiplied by 2 and x-coordinate has to be kept as it is.

Example 4 :

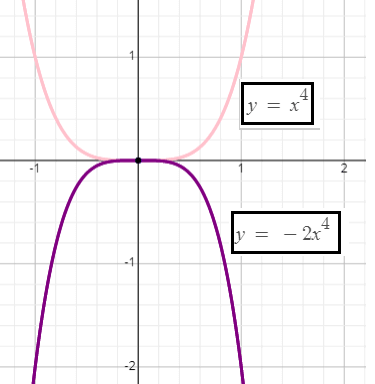
f(x) = -2x⁴

Solution :

For the given function f(x), the basic function is g(x) = x⁴.

Then, the given function can be written as

f(x) = -2g(x)

On the right side, since g(x) is multiplied by -2, we have to do the following two transformations.

g(x) multiplied by 2 ----> vertical stretch by a factor 2

negative sign in front of 2g(x) ----> reflection over x-axis

To get the graph of the given function f(x) on the interval [-1.3, 1.3], we have to strech the basic function g(x) verticaly by a factor of 2. That is, y-coordinate of each point on the basic function has to be multiplied by 2 and x-coordinate has to be kept as it is. Then, we have to reflect the graph over x-axis.

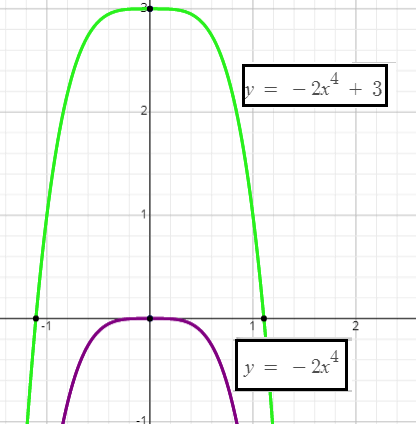
Example 5 :

f(x) = -2x⁴ + 3

Solution :

For the given function f(x), the basic function is g(x) = x⁴.

Then, the given function can be written as

f(x) = -2g(x) + 3

On the right side, since g(x) is multiplied by -2 and 3 added to it, we have to do the following three transformations.

g(x) multiplied by 2 ----> vertical stretch by a factor 2

negative sign in front of 2g(x) ----> reflection over x-axis

3 is added to -2g(x) ----> vertical translation by 3 units up

To get the graph of the given function f(x) on the interval [-1.3, 1.3], we have to strech the basic function g(x) verticaly by a factor of 2. That is, y-coordinate of each point on the basic function has to be multiplied by 2 and x-coordinate has to be kept as it is. Then, we have to reflect the graph over x-axis. Finally, we have to shift the graph vertically up by 3 units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.