HOW TO SKETCH SQUARE ROOT FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
When we are sketching the graph of functions either by hand or through any graphing software we cannot show the entire graph. Only a part of the graph can be sketched.
A crucial question is which part of the curve we need to show and how to decide that part. To decide on this we use the derivatives of functions. We enlist few guidelines for determining a good viewing rectangle for the graph of a function. They are :
(i) The domain and the range of the function.
(ii) The intercepts of the cure (if any).
(iii) Critical points of the function.
(iv) Local extrema of the function.
(v) Intervals of concavity.
(vi) Points of inflections (if any).
(vii) Asymptotes of the curve (if exists)
Sketch the graphs of the following functions.
Problem 1 :
y = x√(4-x)
Solution :
Domain and range :
Possible values of x are (-∞, 3) ==> Domain
y values are (-∞, 4) ==> Range
Intercepts :
To find x intercept, put y = 0
x√(4-x) = 0
|
x = 0 |
√(4-x) = 0 4-x = 0 x = 4 |
x intercepts are 0 and 4.
y-intercept :
Put x = 0
y = 0
Critical points :
f(x) = x√(4-x)
f'(x) = x(1/2√(4-x))(-1) + √(4-x) (1)
f'(x) = -x/2√(4-x) + √(4-x)
f'(x) = [-x+2(4-x)]/2√(4-x)
f'(x) = (-x+8-2x)/2√(4-x)
f'(x) = (8-3x)/2√(4-x)
f'(x) = 0
(8-3x)/2√(4-x) = 0
3x = 8
x = 8/3
Plotting these points on the number line and dividing into intervals, we get (-∞, 8/3) and (8/3, ∞).
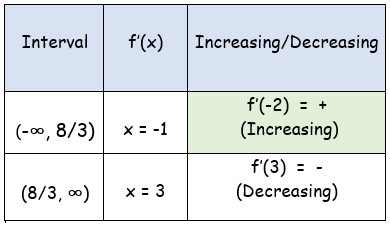
Local extrema :
f'(x) = (8-3x)/2√(4-x)
u = 8-3x and v = 2√(4-x)
u' = -3 and v' = -1/√(4-x)
f''(x) = [2√(4-x)(-3)-(8-3x)(-1/√(4-x))] /4(4-x)
f''(x) = (3x-16)/4(4-x)√(4-x)
f''(8/3) = - < 0 (Maximum)
Maximum value at x = 8/3 :
y = x√(4-x)
y = (8/3)√(4-(8/3))
y = (8/3)√(4/3)
y = 16/3√3
So, the maximum point is (8/3, 16/3√3).
Intervals of concavity :
f''(x) = (3x-16)/4(4-x)√(4-x)
f''(x) = 0
3x-16 = 0
x = 16/3
It is not in the domain, so it has no real value on.
Point of inflection :
There is no point of inflection.
Asymptotes :
As x ->∞, y -> ±∞

Identify the domain and range of each. Then sketch the graph.
Problem 2 :
y = -2√(x + 1)
Solution :
Domain and range :
Possible values of x are (-1, ∞) ==> Domain
y values are (0, -∞) ==> Range
Intercepts :
To find x intercept, put y = 0
-2√(x + 1) = 0
√(x + 1) = 0
x + 1 = 0
x = -1
x intercept is at x = -1.
y-intercept :
Put x = 0
y = -2√(x + 1)
y = -2√(0 + 1)
y = -2
Comparing with y = a√(x - h) + k,
we get move the graph of parent function 1 unit to the left and there is no vertical translation.
Reflection about x-axis and 2 units of vertical stretch.
By applying some inputs, we will get the outputs.
y = -2√(x + 1)
|
When x = -1 y = 0 |
When x = 0 y = -2 |
When x = 1 y = -2.828 |
|
When x = 2 y = -2√3 |
When x = 3 y = -2√4 y = -4 |
The set of ordered pairs are (-1, 0) (0, -2) (1, -4) (2, -2√3) and (3, -4).
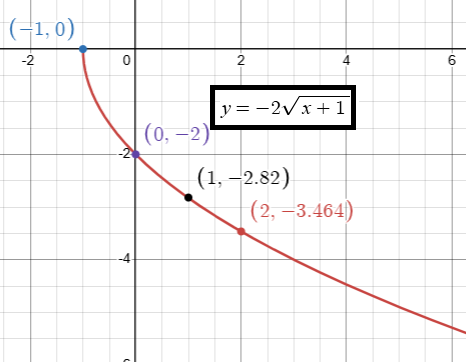
How would each of the following graphs change in relation to the parent graph?
Problem 3 :
y = √(x - 3)
Solution :
Domain and range :
(x - 3) ≥ 0
x ≥ 3
Possible values of x are (3, ∞) ==> Domain
y values are (0, ∞) ==> Range
Intercepts :
To find x intercept, put y = 0
√(x - 3) = 0
x - 3 = 0
x = 3
x intercept is at x = 3.
y-intercept :
Put x = 0
y = √(0 - 3)
There is no x-intercept
Comparing with y = a√(x - h) + k,
we get move the graph of parent function should be moved 3 units to the right.
y = √(x - 3)
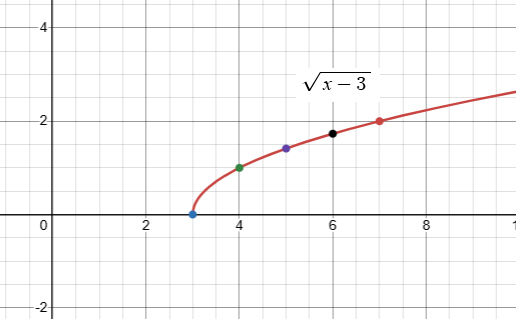
Problem 4 :
y = 2√(x + 2) - 3
Solution :
Domain and range :
(x + 2) ≥ 0
x ≥ 2
Possible values of x are (2, ∞) ==> Domain
y values are (0, ∞) ==> Range
Intercepts :
To find x intercept, put y = 0
2√(x + 2) - 3 = 0
2√(x + 2) = 3
√(x + 2) = 3/2
x + 2 = 9/4
x = (9/4) - 2
x = 1/4
x intercept is at x = 1/4
y-intercept :
Put x = 0
y = 2√(0 + 2) - 3
y = 2√2 - 3
= 2(1.414) - 3
= 2.828 - 3
= -0.172
y-intercept is (0, -0.172)
Comparing with y = a√(x - h) + k,
we get move the graph of parent function,
- Vertical stretch of 2 units
- Moving the graph 2 units left
- Moving the graph 3 units down.
y = 2√(x + 2) - 3
|
When x = -2 y = -3 |
When x = -1 y = 2 - 3 = -1 |
When x = 0 y = 2√(0 + 2) - 3 y = 2√2 - 3 |
|
When x = 6 y = 2√(6 + 2) - 3 y = 4√2 - 3 |
When x = 7 y = 2√9 - 3 y = 3 |
The ordered pairs are (-2, -3) (-1, -1) (0, 2√2 - 3) (6, 4√2 - 3) (7, 3).
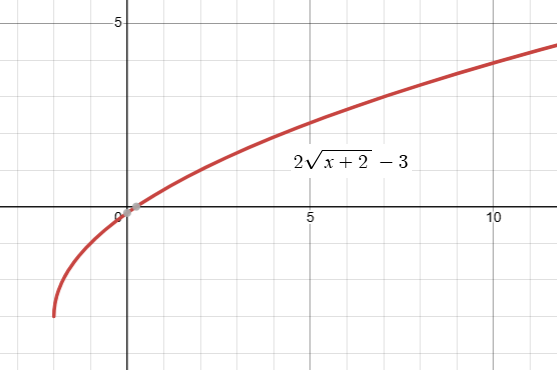
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part -27)
Feb 28, 26 07:46 PM
Digital SAT Math Problems and Solutions (Part -27) -
Digital SAT Math Problems and Solutions (Part - 26)
Feb 28, 26 06:28 PM
Digital SAT Math Problems and Solutions (Part - 26) -
Digital SAT Math Problems and Solutions (Part - 25)
Feb 28, 26 07:21 AM
Digital SAT Math Problems and Solutions (Part - 25)