HOW TO SKETCH A GRAPH OF A FUNCTION WITH LIMITS

About "How to Sketch a Graph of a Function With Limits"

How to Sketch a Graph of a Function With Limits :

Here we are going to see how to sketch a graph of a function with limits.

Question 1 :

Sketch the graph of a function f that satisfies the given values :

f(0) is undefined

lim _{x -> 0} f(x)  =  4

f(2)  =  6

lim _{x -> 2} f(x)  =  3

Solution :

From the given question,

• We understood that the functions is undefined when x = 0.
• When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4.
• When x = 2, the value of y will be 6.
• When the value of x approaches 2 from left hand side and right hand side, limit value will approaches to 3.

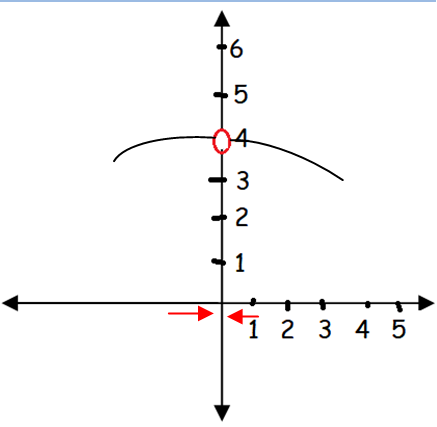
The value of x approaches from left and right, the limit will approach the value 4.

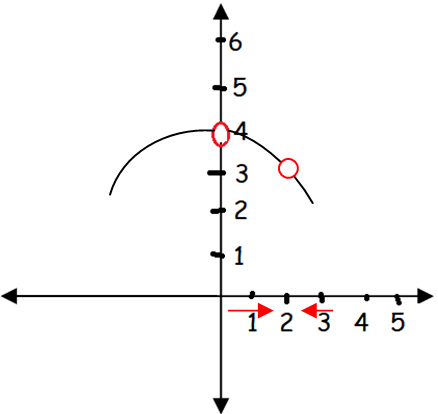
When x approaches 2 from left and right, the limit will approaches to 3. The picture given above will illustrate the condition.

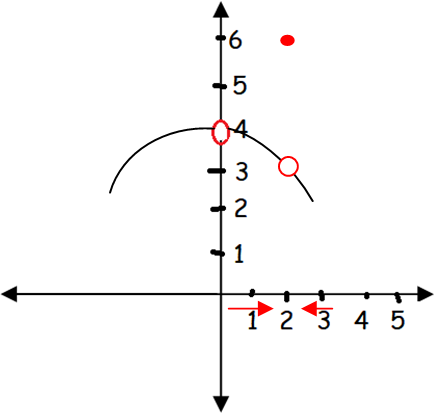
When x = 2, f(x) that is the value of y will be 6.

Hence the picture given above is the required graph of the statements given.

Question 2 :

Sketch the graph of a function f that satisfies the given values :

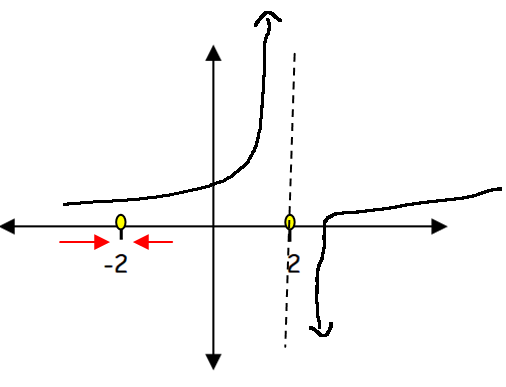
f(-2)  =  0

f(2)  =  0

lim _{x -> -2} f(x)  =  0

lim _{x -> 2} f(x)  does not exists

Solution :

From the given question,

When x = -2, the value of y will be 0.

When x = 2, the value of y will be 0.

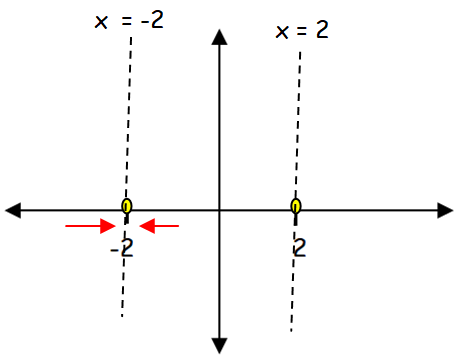
When x tends to 2, the function does not exist. To show this, we have to show the graph with different values of y.

Question 3 :

Write a brief description of the meaning of the notation lim _{x -> 8} f(x)  =  25

Solution :

When x approaches from left side and right side, the value of limit will approaches 25.

Question 4 :

If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?

Solution :

The given statement represents, when x = 2, the value of y will be 4.

Case 1 :

When x approaches from left side and right side, we will get same values approximately, or

Case 2 :

When x approaches from left side and right side, we will  get different values.

Hence, we cannot conclude anything about the limit of f(x) as x approaches 2?

Question 5 :

If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning.

Solution :

Given :

lim _{x -> 2} f(x)  =  4

From this, we may understand that

when x approaches 2 from left side and right side, the limit will approaches to 4.  

Hence we cannot conclude anything about f(2).

Question 6 :

Evaluate : 

lim x->3 (x² -9)/(x - 3) if it exists by finding f(3⁺) and f(3^-)

Solution :

   =  im _x->3 (x² -9)/(x - 3)

   =  im _x->3 (x + 3)(x - 3)/(x - 3)

   =  im _x->3 (x + 3)

Question 7 :

Verify the existence of lim _{x -> 1} f(x)

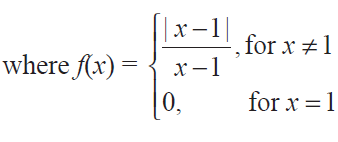
Solution :

If the limit x -> 1 exists, then

lim _{x-> 1}- f(x)  =  lim _{x-> 1}+ f(x)

Since lim _{x-> 1}- f(x)  ≠  lim _{x-> 1}+ f(x), the limit does not exists.

After having gone through the stuff given above, we hope that the students would have understood, "How to Sketch a Graph of a Function With Limits"

Apart from the stuff given in "How to Sketch a Graph of a Function With Limits",  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.