SIMPLIFYING RADICAL EXPRESSIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The following steps will be useful to simplify any radical expressions.
Step 1 :
Decompose the number inside the radical into prime factors.
Step 2 :
If you have square root (√), you have to take one term out of the square root for every two same terms multiplied inside the radical.
Step 3 :
If you have cube root (3√), you have to take one term out of cube root for every three same terms multiplied inside the radical.
Step 4 :
If you have fourth root (4√), you have to take one term out of fourth root for every four same terms multiplied inside the radical.
Step 5 :
Combine the radical terms using mathematical operations.
Example :
√18 + √8 = √(3 ⋅ 3 ⋅ 2) + √(2 ⋅ 2 ⋅ 2)
√18 + √8 = 3√2 + 2√2
√18 + √8 = 5√2
Solved Examples
Example 1 :
Simplify the radical expression :
√169 + √121
Solution :
Decompose 169 and 121 into prime factors using synthetic division.
|
√169 = √(13 ⋅ 13) √169 = 13 |
√121 = √(11 ⋅ 11) √121 = 11 |
So, we have
√169 + √121 = 13 + 11
√169 + √121 = 24
Example 2 :
Simplify the radical expression :
√20 + √320
Solution :
Decompose 20 and 320 into prime factors using synthetic division.
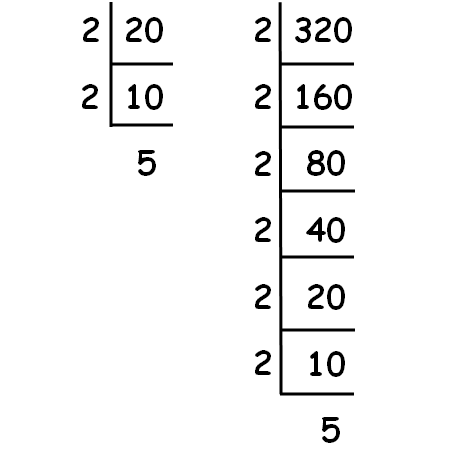
|
√20 = √(2 ⋅ 2 ⋅ 5) √20 = 2√5 |
√320 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) √320 = 2 ⋅ 2 ⋅ 2 ⋅ √5 √320 = 8√5 |
So, we have
√20 + √320 = 2√5 + 8√5
√20 + √320 = 10√5
Example 3 :
Simplify the radical expression :
√117 - √52
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
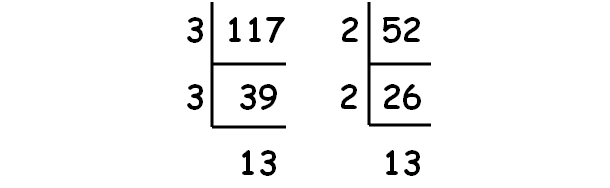
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
So, we have
√117 - √52 = 3√13 - 2√13
√117 + √52 = √13
Example 4 :
Simplify the radical expression :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
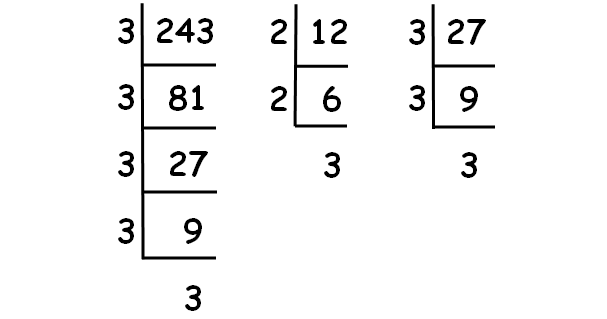
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
So, we have
√243 - 5√12 + √27 = 9√3 - 5(2√3) + 3√3
Simplify.
√243 - 5√12 + √27 = 9√3 - 10√3 + 3√3
√243 - 5√12 + √27 = 2√3
Example 5 :
Simplify the radical expression :
-√147 - √243
Solution :
Decompose 147 and 243 into prime factors using synthetic division.
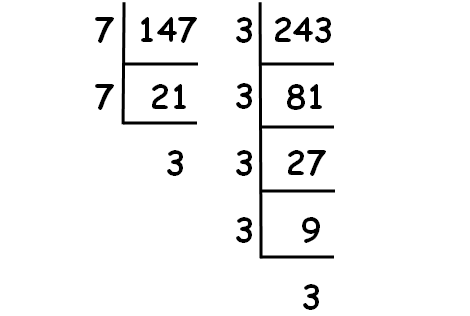
√147 = √(7 ⋅ 7 ⋅ 3) = 7√3
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
So, we have
-√147 - √243 = -7√3 - 9√3
-√147 - √243 = -16√3
Example 6 :
Simplify the radical expression :
(√13)(√26)
Solution :
Decompose 13 and 26 into prime factors.
13 is a prime number. So, it can't be decomposed anymore.
√26 = √(2 ⋅ 13) = √2 ⋅ √13
So, we have
(√13)(√26) = (√13)(√2 ⋅ √13)
(√13)(√26) = (√13 ⋅ √13)√2
(√13)(√26) = 13√2
Example 7 :
Simplify the radical expression :
(3√14)(√35)
Solution :
Decompose 14 and 35 into prime factors.
√14 = √(2 ⋅ 7) = √2 ⋅ √7
√35 = √(5 ⋅ 7) = √5 ⋅ √7
So, we have
(3√14)(√35) = 3( √2 ⋅ √7)(√5 ⋅ √7)
(3√14)(√35) = 3(√7 ⋅ √7)(√2 ⋅ √5)
(3√14)(√35) = 3(7)√(2 ⋅ 5)
(3√14)(√35) = 21√10
Example 8 :
Simplify the radical expression :
(8√117) ÷ (2√52)
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
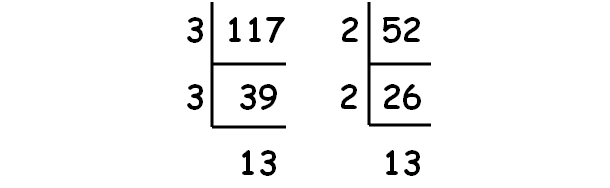
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(8√117) ÷ (2√52) = 8(3√13) ÷ 2(2√13)
(8√117) ÷ (2√52) = 24√13 ÷ 4√13
(8√117) ÷ (2√52) = 24√13 / 4√13
(8√117) ÷ (2√52) = 6
Example 9 :
Simplify the radical expression :
(8√3)2
Solution :
(8√3)2 = 8√3 ⋅ 8√3
(8√3)2 = (8 ⋅ 8)(√3 ⋅ √3)
(8√3)2 = (64)(3)
(8√3)2 = 192
Example 10 :
Simplify the radical expression :
(√2)3 + √8
Solution :
(√2)3 + √8 = (√2 ⋅ √2 ⋅ √2) + √(2⋅ 2 ⋅ 2)
(√2)3 + √8 = (2 ⋅ √2) + 2√2
(√2)3 + √8 = 2√2 + 2√2
(√2)3 + √8 = 4√2
Example 11 :
Simplify :
4√(x4/16)
Solution :
4√(x4/16) = 4√(x4) / 4√16
4√(x4/16) = 4√(x ⋅ x ⋅ x ⋅ x) / 4√(2 ⋅ 2 ⋅ 2 ⋅ 2)
4√(x4/16) = x / 2
Example 12 :
Simplify :
3√(125p6q3)
Solution :
3√(125p6q3) = 3√(5 ⋅ 5 ⋅ 5 ⋅ p2 ⋅ p2 ⋅ p2 ⋅ q ⋅ q ⋅ q)
3√(125p6q3) = 5p2q
Example 13 :
If √(0.9 ⋅ 0.09 ⋅ x) = 0.9 ⋅ 0.9√3, then the value of x/3 is :
Solution :
√(0.9 ⋅ 0.09 ⋅ x) = 0.9 ⋅ 0.9√3
Squaring on both sides
(√(0.9 ⋅ 0.09 ⋅ x))2 = (0.9 ⋅ 0.9)2 (√3)2
(0.9 ⋅ 0.09 ⋅ x) = (0.9 ⋅ 0.9)2 3
x/3 = (0.9 ⋅ 0.9)2 / (0.9 ⋅ 0.09)
x/3 = 0.81/(0.9 ⋅ 0.09)
x/3 = 10
Example 14 :
Find the value of (√1521/11) ⋅ (11/√196)
Solution :
= (√1521/11) ⋅ (11/√196)
By cancelling the numerator and denominator, we get
= (√1521/√196)
= √(39⋅39)/√(14 ⋅ 14)
= 39/14
Example 15 :
Find the value of [ √(7√7√7√7) ]
Solution :
= [ √(7√(7√(7√(7))) ]
Here inside a square root, we have square root of 7 as four times.
= [7 [7 [7 (7)1/2]^1/2]^1/2]^1/2
= [7 [7 [(7)3/2]^1/2]^1/2]^1/2
= [7 [7 (7)3/4]^1/2]^1/2
= [7 [71 + 3/4]^1/2]^1/2
= [7 [77/4]^1/2]^1/2
= [7 ⋅ 77/8]]^1/2
= [7 1 + 7/8]^1/2
= [7 15/8]^1/2
= 7 15/16
Example 16 :
9 √x = √12 + √147, then x is
Solution :
9 √x = √12 + √147
Doing possible simplification, we get
9 √x = √(2⋅2⋅3) + √(3⋅7⋅7)
9 √x = 2√3 + 7√3
9 √x = 9√3
By comparing the corresponding terms, we get
√x = √3
x = 3
So, the value of x is 3.
Example 17 :
Find the value of √2304 + √23.04 + √0.2304
Solution :
= √2304 + √23.04 + √0.2304
√2304 = √(48 ⋅ 48)
= 48
√23.04 = √2304/100
= √(48 ⋅ 48)/(10 ⋅ 10)
= 48/10
= 4.8
√0.2304 = √(2304/10000)
= √(48⋅48)/(100⋅100)
= 48/100
= 0.48
√2304 + √23.04 + √0.2304 = 48 + 4.8 + 0.48
= 53.28
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

