HOW TO REPRESENT DISPLACEMENT GRAPHICALLY IN VECTOR

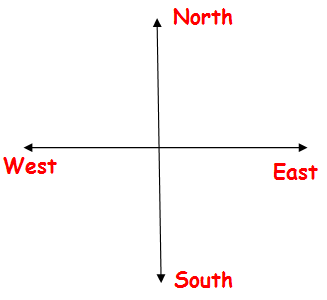
If we want represent displacement in a graph, first we have to draw the coordinate axis and mark the directions.

In the right corner - Mark the direction (East)

In the left corner - Mark the direction (West)

In the top corner - Mark the direction (North)

In the bottom corner - Mark the direction (South)

Key Concept

1. North of west means, it travels from west to north. To represent the particular angle, move the horizontal line to the north side clockwise.

2. West of north means, it travels from north to west. To represent the particular angle, move the vertical line to the west side anticlockwise.

Example 1 :

Represent graphically the displacement of

45 cm 30° north of east

Solution :

To represent the above statement graphically, we have to mark the coordinate axis and write the directions.

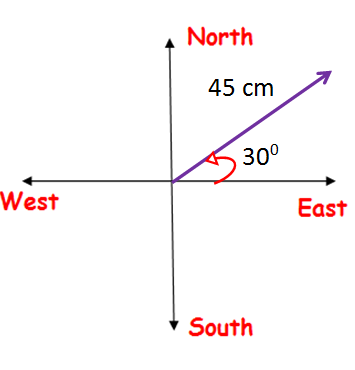
North of east means, it travels from east to north. To represent the particular angle, move the horizontal line to the north side anticlockwise.

Example 2 :

Represent graphically the displacement of

80 km  60° south of west

Solution :

To represent the above statement graphically, we have to mark the coordinate axis and write the directions.

South of west means, it travels from west to south To represent the particular angle, move the horizontal line to the south side anticlockwise.

Example 3 :

Prove that the relation R defined on the set V of all vectors by ‘ a vector R b vector if a vector = b vector is an equivalence relation on V.

Solution :

In order to prove the given is in equivalence relation, we have to prove there exists, reflexive, symmetric and transitive.

R is said to be reflexive if a is related to a for all a ∈ S

Example 4 :

Let a vector and b vector be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are (a vector + 2b vector)/3 and (b vector + 2a vector)/3.

Solution :

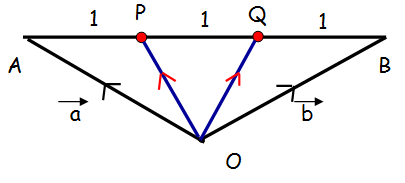
OA  =  a vector, OB  =  b vector

The point P divides the line segment joining the points AB in the ratio 1 : 2 (internally)

  =  (n a  vector + m b vector)/ (n + m) 

  =  (nOB + mOA)/(n + m)

  =  [1(a vector) + 2(b vector)]/ (1 + 2)

  =  (a vector + 2 b vector)/3

The point Q divides the line segment joining the points AB in the ratio 2 : 1 (internally)

  =  (nOB + mOA)/(n + m)

  =  [2(a vector) + 1(b vector)]/ (2 + 1)

  =  (2a vector + b vector)/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.