HOW TO PROVE TWO TRIANGLES SIMILAR

If the measures of the corresponding sides of two triangles are proportional or the measures of their corresponding angles are equal, then the two triangles are similar. 

In triangles ABC and DEF, if 

AB/DE  =  BC/EF  =  AC/DF

then, 

ΔABC ∼ ΔDEF

In triangles ABC and DEF, if 

∠A  =  ∠D

∠B  =  ∠E

∠C  =  ∠F

then, 

ΔABC ∼ ΔDEF

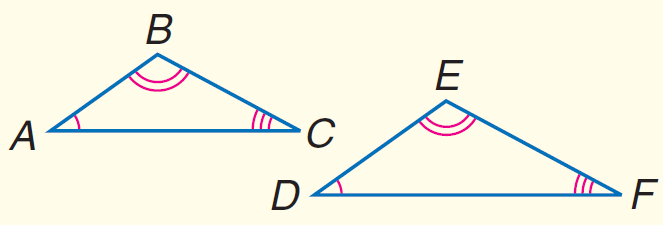
Examples 

Example 1 :

Determine whether the two triangles shown below are similar. Justify your answer.

Solution :

The angles BAC and DFE  are congruent.To prove the above triangles are similar, we need to prove one more pairs of angles are equal.

To check whether the angles BCA and DEF are equal, let us find the measure of angle BCA from triangle ABC.

∠BAC + ∠ABC + ∠BCA  =  180

21 + 105 +  ∠BCA  =  180

126 + ∠BCA  =  180

∠BCA  =  180 - 126

∠BCA  =  54⁰

∠BCA  =  ∠DEF 

So, the triangles ABC and DEF are similar.

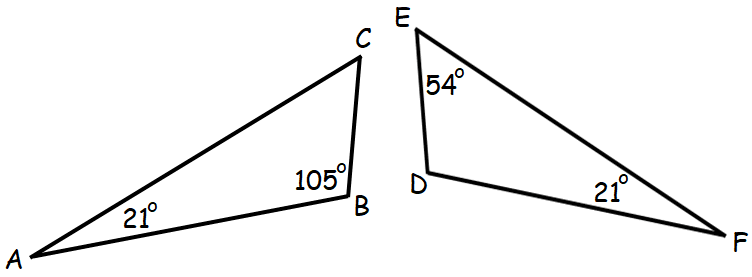
Example 2 :

Determine whether the two triangles shown below are similar. Justify your answer.

Solution :

The angles ∠ACB and ∠FDE are congruent.To prove the above triangles are similar, we need to prove one more pairs of angles are equal.

To check whether the angles ABC and DEF are equal, let us find the measure of angle ABC from triangle ABC.

∠ABC + ∠BAC + ∠ACB  =  180

∠ABC + 79 +  60  =  180

∠ABC + 139  =  180

∠ABC  =  180 - 139

∠ABC  =  41

∠ABC  ≠  ∠DEF 

Hence the above triangles ABC and DEF are not similar.

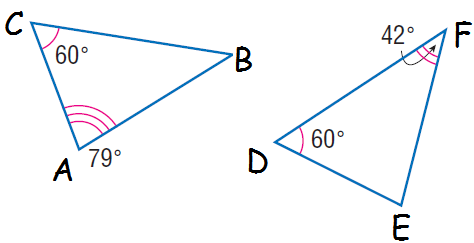
Example 3 :

Determine whether the two triangles shown below are similar. Justify your answer.

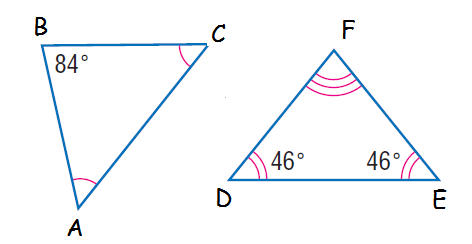
Solution :

To check whether the above triangles are similar, we need to find the missing angles of triangle ABC.

∠ABC + ∠BAC + ∠ACB  =  180

84 +  ∠BAC + ∠ACB  =  180

2∠BAC  =  180 - 84

2∠BAC  =  96

∠BAC  =  96/2

∠BAC  =  48  =  ∠ACB

The corresponding angles of BAC  and DEF are not same.

So, the above triangles are not similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.