HOW TO PROVE THE GIVEN POINTS ARE COLLINEAR

Here we are going to see how to prove the given Points are collinear.

To prove the the given three points are colinear, we may use the following methods.

(i) Using slope

(ii)  Equation of the line

(iii)  Using the formula for area of triangle

(iv)  Using determinant

Example

Show that the points (1, 3), (2, 1) and (1/2, 4) are collinear, by using (i) concept of slope (ii) using a straight line and (iii) any other method

Solution :

Let the points be A (1, 3) B (2, 1) and C (1/2, 4)

If the given points are collinear, then

Slope of AB  =  Slope of BC

Slope of a line :

m  =  (y₂ - y₁)/(x₂ - x₁)

Hence the given points are collinear.

(ii) using a straight line 

If the equations formed using any two points on the line will be equal, then we may decide that the given points are collinear.

A (1, 3) B (2, 1)

Equation of AB :

(y−y₁)/(y₂−y₁)  =  (x−x₁)/(x₂-x₁)

(y - 3)/(1 - 3)  =  (x - 1)/(2 - 1)

(y - 3)/(-2)  =  (x - 1)/1

y - 3  =  -2 (x - 1)

y - 3  =  -2x + 2

y  =  -2x + 2 + 3

y  =  -2x + 5

Equation of BC :

B (2, 1) and C (1/2, 4)

(y−y₁)/(y₂−y₁)  =  (x−x₁)/(x₂-x₁)

(y - 1)/(4 - 1)  =  (x - 2)/((1/2) - 2)

(y - 1)/3  =  (x - 2)/(-3/2)

y - 1  =  -2 (x - 2)

y - 1  =  -2x + 4

y  =  -2x + 4 + 1

y  =  - 2x + 5

Hence the given points are colinear.

(iii) any other method

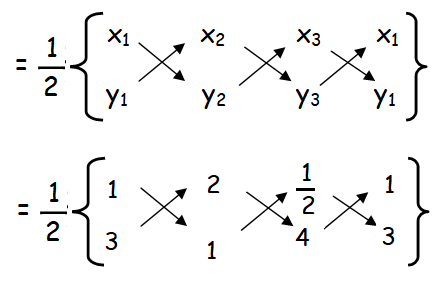
  =  (1/2)  [(1 + 8 + 3/2) - (6 + 1/2 + 4)]

  =  (1/2)  [(9 + 3/2) - (10 + 1/2)]

  =  (1/2)  [(21/2) - (21/2)]

  =  (1/2)  [0]

  =  0 

Hence the given points are collinear.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.